
【题目】如图1,在![]() 中,
中,![]() 是
是![]() 的直径,
的直径,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,试求
,试求![]() 的长;
的长;
(3)如图2,点![]() 是弧
是弧![]() 的中点,连结
的中点,连结![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD的对角线AC、BD相交于点O,∠BDC=45°,过点B作BH⊥DC交DC的延长线于点H,在DC上取DE=CH,延长BH至F,使FH=CH,连接DF、EF.

(1)若AB=2,AD=![]() ,求BH的值;
,求BH的值;
(2)求证:AC=![]() EF.
EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为![]() ,按表格要求确定奖项.
,按表格要求确定奖项.

(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌手机销售公司有营销员14人,销售部为制定营销人员月销售手机定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 165 | 80 | 50 | 40 |
人 数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)求这14位营销员该月销售该品牌手机的平均数、中位数和众数.
(2)销售部经理把每位营销员月销售量定为100台,你认为是否合理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC内接于⊙O,I为其内心,AI的延长线交⊙O于D,连OD交BC于E.
(1)求证: OD⊥ BC;
(2)若∠BOC=∠BIC,求∠BAC的度数;
(3)①若DE=2,BE=4,①求⊙O的半径r.
②当点A在优弧BAC上移动时,OI是否有最小值,如有请求出最小值,如没有请说明理由.
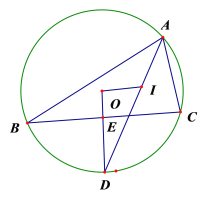
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,点D在AC上(CD<![]() AC),连接BD.操作:以A为圆心,AD长为半径画弧,交BD于点E,连接AE.
AC),连接BD.操作:以A为圆心,AD长为半径画弧,交BD于点E,连接AE.
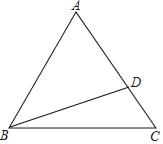
(1)请补全图形,探究∠BAE、∠CBD之间的数量关系,并证明你的结论;
(2)把BD绕点D顺时针旋转60°,交AE于点F,若EF=mAF,求![]() 的值(用含m的式子表示).
的值(用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,三角形纸片![]() ,先将该纸片沿过点
,先将该纸片沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在斜边
落在斜边![]() 上的一点
上的一点![]() 处,折痕记为
处,折痕记为![]() (如图1).剪去
(如图1).剪去![]() 后得到双层
后得到双层![]() (如图2),再沿着过
(如图2),再沿着过![]() 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为______
某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为______![]()
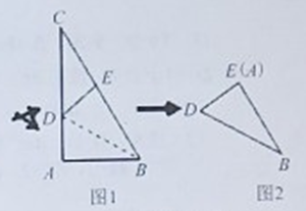
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°)
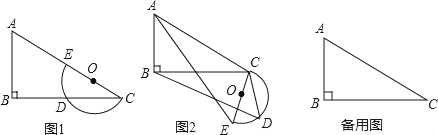
(1)当α=0°时,连接DE,则∠CDE= °,CD= ;
(2)试判断:旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)若m=10,n=8,当α=∠ACB时,求线段BD的长;
(4)若m=6,n=4![]() ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=12,动点M从A点出发,以每秒1个单位长度的速度沿着AC方向向C点运动,动点N从C点出发,以每秒2个单位长度的速度沿着CB方向向B点运动,如果M,N两点同时出发,当M到达C点处时,两点都停止运动,设运动的时间为t秒,四边形AMNB的面积为S.
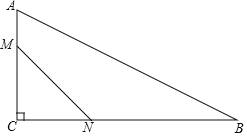
(1)用含t的代数式表示:CM= ,CN= .
(2)当t为何值时,△CMN与△ABC相似?
(3)求S和t的关系式(写出自变量t的取值范围);当t取何值时,S的最小,并求最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com