
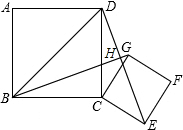
 将边长为$\sqrt{5}$的正方形ABCD与边长$\sqrt{2}$为的正方形CEFG如图摆放,连BG、DE.将正方形CEFG绕点C逆时针旋转.
将边长为$\sqrt{5}$的正方形ABCD与边长$\sqrt{2}$为的正方形CEFG如图摆放,连BG、DE.将正方形CEFG绕点C逆时针旋转.分析 (1)利用△BOD∽△COG求出线段BO、OC、OD、OG,在RT△BGE中利用勾股定理即可求BE.
(2)图2中,当CG⊥BG时,F与H重合,此时点H到直线BC的距离最大,作HM⊥BC垂足为M,利用△BCG∽△BFM即可求出最大值FM.
解答 解:(1)如图1, ∵四边形ABCD、四边形CGEF都是正方形,
∵四边形ABCD、四边形CGEF都是正方形,
∴BC=CD=$\sqrt{5}$,CG=CE=$\sqrt{2}$,∠BCD=∠GCE=90°,∠DEC=∠CGE=45°,∠BDC=45°,
∴BD=$\sqrt{10}$,GE=2,
∴∠BCG=∠DCE,
在△BCG和△DCE中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCG=∠DCE}\\{CG=CE}\end{array}\right.$,
∴△BCG≌△DCE,
∴∠BGC=∠DEC=45°,
∴∠BGE=∠BGC+∠CGE=90°,
∵∠DOB=∠GOC,∠BDO=∠OGC,
∴△BDO∽△CGO,
∴$\frac{BD}{CG}=\frac{BO}{OC}=\frac{DO}{OG}$=$\frac{\sqrt{10}}{\sqrt{2}}$=$\sqrt{5}$,
设OC=k,则BO=$\sqrt{5}$k,∵BO2=OC2+BC2,
∴5k2=5+k2,
∴k=$\frac{\sqrt{5}}{2}$,
∴OC=OD=$\frac{\sqrt{5}}{2}$,BO=$\frac{5}{2}$,OG=$\frac{1}{2}$,
∴BG=BO+OG=3,
在RT△BGE中,BG=3,EG=2,
∴BE=$\sqrt{B{G}^{2}+G{E}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$.
故答案为$\sqrt{13}$
(2) 如图2,当CG⊥BG时,F与H重合,此时点H到直线BC的距离最大,作HM⊥BC垂足为M.
如图2,当CG⊥BG时,F与H重合,此时点H到直线BC的距离最大,作HM⊥BC垂足为M.
在RT△BCG中,∵BC=$\sqrt{5}$,GC=$\sqrt{2}$,
∴BG=$\sqrt{B{C}^{2}-G{C}^{2}}$=$\sqrt{3}$,BH=$\sqrt{3}$+$\sqrt{2}$,
∵∠CBG=∠MBF,∠CGB=∠FMB,
∴△BCG∽△BFM,
∴$\frac{GC}{HM}=\frac{BC}{BF}$,
∴$\frac{\sqrt{2}}{HM}=\frac{\sqrt{5}}{\sqrt{3}+\sqrt{2}}$,
∴HM=$\frac{\sqrt{30}+2\sqrt{5}}{5}$,
∴点H到直线BC的距离的最大值为$\frac{\sqrt{30}+2\sqrt{5}}{5}$.
故答案为$\frac{\sqrt{30}+2\sqrt{5}}{5}$.
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质、以及旋转等知识,正确画出图形,灵活运用三角形全等或相似是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x$\sqrt{-x}$ | B. | -x$\sqrt{-x}$ | C. | x$\sqrt{x}$ | D. | -x$\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
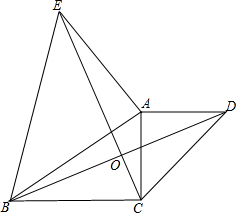 如图,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABE,等腰直角三角形ACD,其中∠BAE=∠CAD=90°,BD与CE相交于点O,则:∠DOE的大小是否会随着∠BAC大小的变化而变化?如不变,请求出∠DOE的大小?如变化,说明理由.
如图,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABE,等腰直角三角形ACD,其中∠BAE=∠CAD=90°,BD与CE相交于点O,则:∠DOE的大小是否会随着∠BAC大小的变化而变化?如不变,请求出∠DOE的大小?如变化,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.直线y=-$\frac{1}{3}$x+1过点B且与y轴交于点D,E为抛物线顶点.若∠DBC=α,∠CBE=β,
如图,抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.直线y=-$\frac{1}{3}$x+1过点B且与y轴交于点D,E为抛物线顶点.若∠DBC=α,∠CBE=β,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b<-a<a<-b | B. | -b<-a<a<b | C. | -a<b<-b<a | D. | -a<-b<a<b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com