
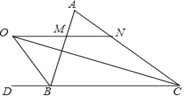
【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
【答案】见解析
【解析】
【试题分析】(1)因为OB是∠ABD的平分线,根据角平分线的定义,得∠0BD=∠OBM,因为MN∥BC,根据两直线平行,内错角相等,得∠0BD=∠BOM,等量代换得:∠OBM=∠BOM,
根据等角对等边,得:MO=MB
(2)因为OC是∠ACB的平分线,根据角平分线的定义,得∠BCO=∠ACO
因为MN∥BC,根据两直线平行,内错角相等,得∠BCO=∠NOC,等量代换得:∠NOC=∠NCO
根据等角对等边,得:NO=NC,由图可知,MN=NO-MO,等量代换得,MN=CN-BM.
【试题解析】
(1)∵OB是∠ABD的平分线.
∴∠0BD=∠OBM.
∵MN∥BC.
∴∠0BD=∠BOM.
∴∠OBM=∠BOM.
∴MO=MB.
(2)∵OC是∠ACB的平分线.
∴∠BCO=∠ACO.
∵MN∥BC.
∴∠BCO=∠NOC.
∴∠NOC=∠NCO.
∴NO=NC.
∵MN=NO-MO.
∴MN=CN-BM.


科目:初中数学 来源: 题型:
【题目】在数学、外语、语文及其他学科中,某校七年级开展了“同学们最喜欢哪门学科”的调查(该校七年级共有200人,每人只能选一项).
(1)调查的问题是什么?调查的对象是谁?
(2)在被调查的200名学生中,有40人最喜欢语文,60人最喜欢数学,80人最喜欢外语,其余的人选择其他.请把七年级的学生最喜欢某学科的人数及其占学生总数的百分比填入下表:
语文 | 外语 | 数学 | 其他 | |
人数 | ||||
占学生总数的百分比 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx-3经过A(-1,0)、B(3,0)两点,与y轴交于C点,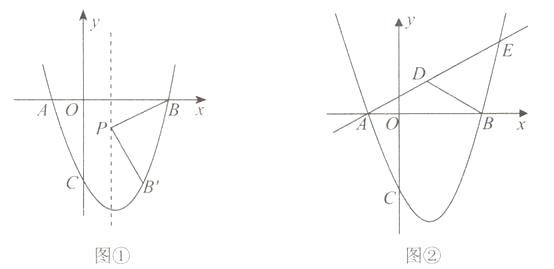
(1)求抛物线的解析式;
(2)如图①,抛物线的对称轴上有一点P,且点P在x轴下方,线段PB绕点P顺时针旋转90°,点B的对应点B′恰好落在抛物线上,求点P的坐标;
(3)如图②,直线y= ![]() x+
x+ ![]() 交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)如图,正方形网格中的每个小正方形边长都是1.
(利用网格线进行画图,别忘了标上字母噢!)
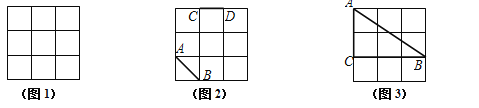
(1) 在图1中,画一个顶点为格点、面积为5的正方形;
(2) 在图2中,已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形;
(要求画出所有符合题意的线段)
(3) 在图3中,找一格点D,满足:①到CB、CA的距离相等;②到点A、C的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,E是AB的中点,且DE⊥AB于点E,∠CAD:∠EAD=1:2,则∠B与∠BAC的度数为( )
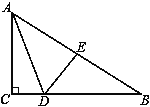
A. 30°,60° B. 32°,58° C. 36°,54° D. 20°,70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,且OC=3OA,点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.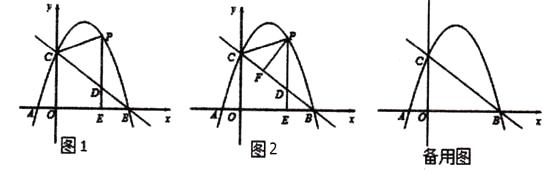
(1)试求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PFD的周长是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四 边形CDPQ能否成为菱形?如果能,请求此时点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知直线
中,已知直线 ![]() (
( ![]() )分别交反比例函数
)分别交反比例函数 ![]() 和
和 ![]() 在第一象限的图象于点
在第一象限的图象于点 ![]() ,
, ![]() ,过点
,过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() ,交
,交 ![]() 的图象于点
的图象于点 ![]() ,连结
,连结 ![]() .若
.若 ![]() 是等腰三角形,则
是等腰三角形,则 ![]() 的值是 .
的值是 . 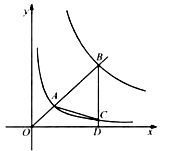
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;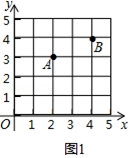
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.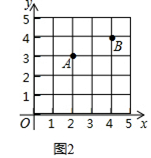
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com