
【题目】如图一块直角三角形ABC,∠B=90°,AB=3,BC=4,截得两个正方形DEFG,BHJN,设S1=DEFG的面积,S2=BHJN的面积,则S1、S2的大小关系是( )
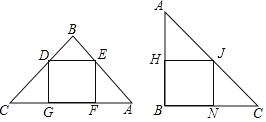
A.S1>S2B.S1<S2C.S1=S2D.不能确定
【答案】B
【解析】
根据勾股定理求出AC,求出AC边上的高BM,根据相似三角形的性质得出方程,求出方程的解,即可求得S1,如图2,根据相似三角形的性质列方程求得HJ=![]() ,于是得到S2=(
,于是得到S2=(![]() )2>(
)2>(![]() )2,即可得到结论.
)2,即可得到结论.
解:如图1,设正方形DEFG的边长是x,
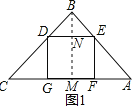
∵△ABC是直角三角形,∠B=90°,AB=3,BC=4,
∴由勾股定理得:AC=5,
过B作BM⊥AC于M,交DE于N,
由三角形面积公式得:![]() BC×AB=
BC×AB=![]() AC×BM,
AC×BM,
∵AB=3,AC=5,BC=4,
∴BM=2.4,
∵四边形DEFG是正方形,
∴DG=GF=EF=DE=MN=x,DE∥AC,
∴△BDE∽△ABC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴x=![]() ,
,
即正方形DEFG的边长是![]() ;
;
∴S1=(![]() )2,
)2,
如图2,
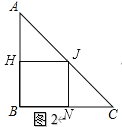
∵HJ∥BC,
∴△AHJ∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴HJ=![]() ,
,
∴S2=(![]() )2>(
)2>(![]() )2,
)2,
∴S1<S2,
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上的一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则下列结论中:

①![]() ;②
;②![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④
;④![]() 正确的是()
正确的是()
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动会期间,甲、乙、丙三位同学参加乒乓球单打比赛,用抽签的方式确定第一场比赛的人选.
(1)若已确定甲参加第一次比赛,求另一位选手恰好是乙同学的概率;
(2)用画树状图或列表的方法,写出参加第一场比赛选手的所有可能,并求选中乙、丙两位同学参加第一场比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .
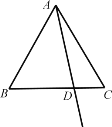
(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
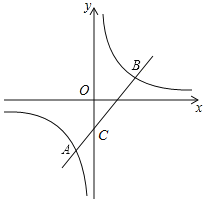
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数y=![]() (k2≠0)的图象交于A(-1,-4)和点B(4,m)
(k2≠0)的图象交于A(-1,-4)和点B(4,m)
(1)求这两个函数的解析式;
(2)已知直线AB交y轴于点C,点P(n,0)在x轴的负半轴上,若△BCP为等腰三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
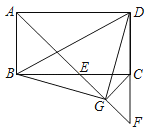
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG.
(1)求证:△DCG≌△BEG;
(2)你能求出∠BDG的度数吗?若能,请写出计算过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到C处有生命迹象.已知A,B两点相距6米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
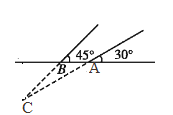
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
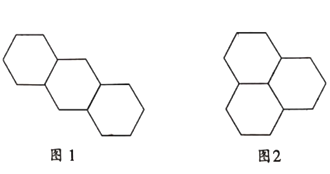
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是_______.有![]() 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则
个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com