
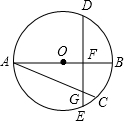
 如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G.
如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G.分析 (1)连接EC,图中相等的应该有半径AO=OB,根据垂径定理即可证明图中应该还有4对相等的线段,所以可得有5对相等线段;
(2)可通过角的关系来判断边的关系,根据EM是圆O的切线,如果我们连接AD、AE,那么∠GEM=∠EAD,现在的关键是证明∠MGE=∠EAD,因为∠MGE=∠EAG+∠DEA,∠DAE=∠EAG+∠DAG,如果要得出∠DAG=∠DEA的话,就能得出∠MGE=∠MEG的结论,而题中告诉了于=,因此这两个角就相等了.由此便可根据等角对等边来得出ME=MG.
解答 解:(1)AO=OB,DF=EF,AC=DE,AG=DG,CG=GE;
(2)ME=MG成立,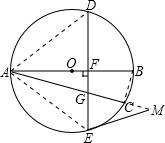
证明:连接AD、AE,
∵$\widehat{AD}=\widehat{CD}$,
∴∠DEA=∠CAD,
∵∠EGM=∠DEA+∠EAM,
∴∠EGM=∠EAM+∠CAD=∠EAD;
∵EM是⊙O的切线,
∴∠GEM=∠EAD,
∴∠EGM=∠GEM,
∴ME=MG.
点评 本题主要考查了切线的性质以及圆周角定理,垂径定理等知识点的综合应用,根据圆周角得出弧相等进而得出相关的角相等是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com