
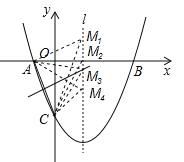
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
【答案】(1)![]() ;(2)P(1,0);(3).
;(2)P(1,0);(3).
【解析】
试题分析:(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可;
(2)由图知:A.B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l与x轴的交点,即为符合条件的P点;
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、③AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
试题解析:(1)将A(﹣1,0)、B(3,0)、C(0,﹣3)代入抛物线![]() 中,得:
中,得: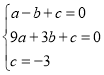 ,解得:
,解得: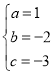 ,故抛物线的解析式:
,故抛物线的解析式:![]() .
.
(2)当P点在x轴上,P,A,B三点在一条直线上时,点P到点A、点B的距离之和最短,此时x=![]() =1,故P(1,0);
=1,故P(1,0);
(3)如图所示:抛物线的对称轴为:x=![]() =1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
=1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =10;
=10;
①若MA=MC,则![]() ,得:
,得:![]() =
=![]() ,解得:m=﹣1;
,解得:m=﹣1;
②若MA=AC,则![]() ,得:
,得:![]() =10,得:m=
=10,得:m=![]() ;
;
③若MC=AC,则![]() ,得:
,得:![]() =10,得:
=10,得:![]() ,
,![]() ;
;
当m=﹣6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,![]() )(1,
)(1,![]() )(1,﹣1)(1,0).
)(1,﹣1)(1,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】高空的气温与距地面的高度有关,某地地面气温为24℃,且已知距离地面高度每升高1km,气温下降6℃.
(1)写出该地空中气温T(℃)与距离地面高度h(km)之间的关系式;
(2)求距地面3km处的气温T.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·无锡中考)如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.

(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】总投资647亿元的西域高铁预计2017年11月竣工,届时成都到西安只需3小时,上午游武侯区,晚上看大雁塔将成为现实,用科学记数法表示647亿元为( )
A.647×108
B.6.47×109
C.6.47×1010
D.6.47×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=-x(x+3-a)+1是关于x的二次函数,当x的取值范围在1≤x≤5时,y在x=1时取得最大值,则实数a的取值范围是( )
A. a=9 B. a=5 C. a≤9 D. a≤5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com