
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
【答案】(1)y=﹣![]() x2+x+4;(2)点E的坐标为(1,
x2+x+4;(2)点E的坐标为(1,![]() ),(3,
),(3,![]() );(3)菱形的边长为4
);(3)菱形的边长为4![]() ﹣4.
﹣4.
【解析】
试题分析:(1)把点A(﹣2,0),点B(4,0),点D(2,4)代入y=ax2+bx+c,用待定系数法求出抛物线解析式即可.(2)分点E在直线CD上方的抛物线上和点E在直线CD下方的抛物线上两种情况,用三角函数求解即可;(3)分CM为菱形的边和CM为菱形的对角线两种情况,用菱形的性质进行计算即可.
试题解析:(1)∵抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),
∴设抛物线解析式为y=a(x+2)(x﹣4),
∴﹣8a=4,
∴a=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() (x+2)(x﹣4)=﹣
(x+2)(x﹣4)=﹣![]() x2+x+4;
x2+x+4;
(2)如图1,
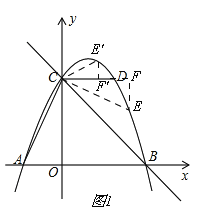
①点E在直线CD上方的抛物线上,记E′,
连接CE′,过E′作E′F′⊥CD,垂足为F′,
由(1)知,OC=4,
∵∠ACO=∠E′CF′,
∴tan∠ACO=tan∠E′CF′,
∴![]() =
=![]() ,
,
设线段E′F′=h,则CF′=2h,
∴点E′(2h,h+4)
∵点E′在抛物线上,
∴﹣![]() (2h)2+2h+4=h+4,
(2h)2+2h+4=h+4,
∴h=0(舍)h=![]()
∴E′(1,![]() ),
),
②点E在直线CD下方的抛物线上,记E,
同①的方法得,E(3,![]() ),
),
点E的坐标为(1,![]() ),(3,
),(3,![]() )
)
(3)①CM为菱形的边,如图2,
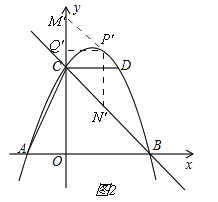
在第一象限内取点P′,过点
P′作P′N′∥y轴,交BC于N′,过点P′作P′M′∥BC,
交y轴于M′,
∴四边形CM′P′N′是平行四边形,
∵四边形CM′P′N′是菱形,
∴P′M′=P′N′,
过点P′作P′Q′⊥y轴,垂足为Q′,
∵OC=OB,∠BOC=90°,
∴∠OCB=45°,
∴∠P′M′C=45°,
设点P′(m,﹣![]() m2+m+4),
m2+m+4),
在Rt△P′M′Q′中,P′Q′=m,P′M′=![]() m,
m,
∵B(4,0),C(0,4),
∴直线BC的解析式为y=﹣x+4,
∵P′N′∥y轴,
∴N′(m,﹣m+4),
∴P′N′=﹣![]() m2+m+4﹣(﹣m+4)=﹣
m2+m+4﹣(﹣m+4)=﹣![]() m2+2m,
m2+2m,
∴![]() m=﹣
m=﹣![]() m2+2m,
m2+2m,
∴m=0(舍)或m=4﹣2![]() ,
,
菱形CM′P′N′的边长为![]() (4﹣2
(4﹣2![]() )=4
)=4![]() ﹣4.
﹣4.
②CM为菱形的对角线,如图3,
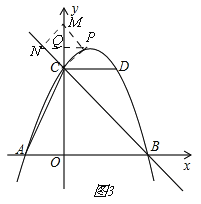
在第一象限内抛物线上取点P,过点P作PM∥BC,
交y轴于点M,连接CP,过点M作MN∥CP,交BC于N,
∴四边形CPMN是平行四边形,连接PN交CM于点Q,
∵四边形CPMN是菱形,
∴PQ⊥CM,∠PCQ=∠NCQ,
∵∠OCB=45°,
∴∠NCQ=45°,
∴∠PCQ=45°,
∴∠CPQ=∠PCQ=45°,
∴PQ=CQ,
设点P(n,﹣![]() n2+n+4),
n2+n+4),
∴CQ=n,OQ=n+2,
∴n+4=﹣![]() n2+n+4,
n2+n+4,
∴n=0(舍),
∴此种情况不存在.
∴菱形的边长为4![]() ﹣4.
﹣4.


科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题:
明明家准备装修房子,房子的部分平面图如图1所示.为了增大房子的使用空间,爸爸想把现在两间卧室之间的非承重墙打掉,之后在打掉的位置做一排衣柜.
爸爸说:“我想测量一下非承重墙的厚度,从而知道打掉这堵墙后可以腾出多少空间.我手里有的工具是教学用量角器、大刻度尺,明明,你帮助爸爸看看应该怎样测量.”
“这堵墙的厚度处处相等吗?”明明说.
爸爸说:“这个没问题,当年收房的时候我就考察过.”
“那我就可以在地面上直接进行测量了.我再问您,每个房间中地面和墙的交线都是垂直或平行的吗?”明明说.
爸爸回答:“是的”.
“那就简单了.我们俩先测出客厅的东西向宽度,再测出每个卧室的东西向宽度,用客厅的宽度减去两个卧室的宽度就是中间这堵非承重墙的厚度.”明明说.
爸爸说:“那不行,客厅和卧室的家具摆得满满的,东西向宽度勉强测到也不准确.你能不能在不借助测量房间宽度或房间内其它家具的前提下,设计一个通过测量和计算得到非承重墙厚度的方案.”
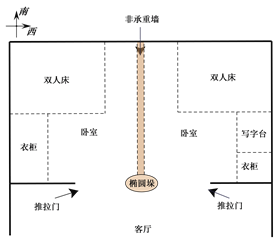

图1 图2
请你利用学到的三角形或四边形的知识帮助明明解决此问题.
要求:(1)在图2中画出测量时用到的示意图,图形要规范;
(2)简要叙述测量过程;
(3)写出测量的依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小美根据学习函数的经验,对函数
的图象与性质.小美根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)下表是y与x的几组对应值.m的值为 ;
x | -2 |
| -1 |
|
|
| 1 | 2 | 3 | 4 | … |
y | 0 |
| -1 |
|
|
|
| m |
|
| … |
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
(1)求抛物线的解析式,并写出其顶点B的坐标;
(2)①当P点运动到A点处时,计算:PO= ,PH= ,由此发现,PO PH(填“>”、“<”或“=”);
②当P点在抛物线上运动时,猜想PO与PH有什么数量关系,并证明你的猜想;
(3)如图2,设点C(1,﹣2),问是否存在点P,使得以P,O,H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.
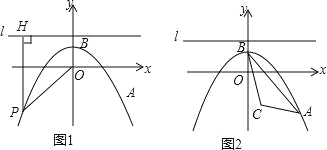
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com