练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在下面的平面直角坐标系中，画出符合下列条件的点：

    （1）画出5个纵坐标比横坐标大2的点，分别标上，，，，．

    （2）画出5个横坐标是纵坐标的2倍的点，分别标上，，，，．

    （3）观察上面两题所画出的点，你有什么发现，分别用语言叙述出来．

    【答案】（1）见解析；（答案不唯一）（2）见解析；（答案不唯一）（3）第（1）小题所画的点都在直线上；第（2）小题所画的点都在直线上．（答案不唯一）

    【解析】

    （1）根据坐标的定义，任意画出5个纵坐标比横坐标大2的点即可；

    （2）根据坐标的定义，任意画出5个横坐标是纵坐标的2倍的点即可；

    （3）观察可知，（1）、(2)两小题各点分别在两条直线上，得出解析式，写出结论即可．

    解：（1）、（2）描点如下图：（答案不唯一）

    （3）第（1）小题所画的点都在直线上；第（2）小题所画的点都在直线上．（答案不唯一）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    问题情境：正方形折叠中的数学

    已知正方形纸片ABCD中，AB=4，点E是AB边上的一点，点G是CE的中点，将正方形纸片沿CE所在直线折叠，点B的对应点为点B′．

    (1)如图1，当∠BCE=30°时，连接BG，B′G，求证：四边形BEB′G是菱形；

    深入探究：

    (2)在CD边上取点F，使DF=BE，点H是AF的中点，再将正方形纸片ABCD沿AF所在直线折叠，点D的对应点为D′，顺次连接B′，G，D′，H，B'，得到四边形B′GD′H．

    请你从A，B两题中任选一题作答，我选择　 　题．

    A题：如图2，当点B'，D′均落在对角线AC上时，

    ①判断B′G与D′H的数量关系与位置关系，并说明理由；

    ②直写出此时点H，G之间的距离．

    B题：如图3，点M是AB的中点，MN∥BC交CD于点N，当点B'，D′均落在MN上时，

    ①判断B′G与D′H的数量关系与位置关系，并说明理由；

    ②直接写出此时点H，G之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

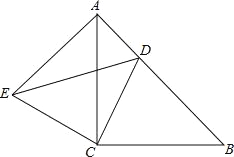
    【题目】如图，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点，

    （1）求证：△ACE≌△BCD；

    （2）若DE=13，BD=12，求线段AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】联想三角形内心的概念，我们可引入如下概念．

    定义：到三角形的两边距离相等的点，叫做此三角形的准内心．

    举例：如图1，若PD=PE，则点P为△ABC的准内心．

    应用：如图2，BF为等边三角形的角平分线，准内心P在BF上，且PF=BP，求证：点P是△ABC的内心．

    探究：已知△ABC为直角三角形，∠C=90°，准内心P在AC上，若PC=AP，求∠A的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

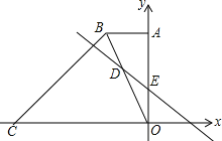
    【题目】如图，在平面直角坐标中，直角梯形OABC的边OC、OA分别在x轴、y轴上，AB∥OC，∠AOC=90°，∠BCO=45°，BC=12，点C的坐标为(-18，0)．

    （1）求点B的坐标；

    （2）若直线DE交梯形对角线BO于点D，交y轴于点E，且OE=4，∠OFE=45°，求直线DE的解析式；

    （3）求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

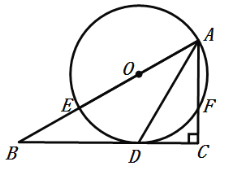
    【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD．

    （1）求证：AD平分∠BAC；

    （2）连接OC,如果∠B=30°,CF=1,求OC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】高高的路灯挂在路边的上方，高傲而明亮，小明拿着一根2米长的竹竿，想量一量路灯的高度，直接量是不可能的．于是，他走到路灯旁的一个地方，竖起竹竿（即AE），这时，他量了一下竹竿的影长（AC）正好是1米，他沿着影子的方向走，向远处走出两根竹竿的长度（即AB=4米），他又竖起竹竿，这时竹竿的影长正好是一根竹竿的长度（即BD=2米）．此时，小明抬头瞧瞧路灯，若有所思地说：“噢，我知道路灯有多高了！”同学们，请你和小明一起解答这个问题：

    （1）在图中作出路灯O的位置，并作OP⊥l于P．

    （2）求出路灯O的高度，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

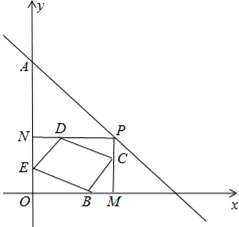
    【题目】如图，已知一次函数y=﹣x+b的图象过点A（0，3），点p是该直线上的一个动点，过点P分别作PM垂直x轴于点M，PN垂直y轴于点N，在四边形PMON上分别截取：PC=MP，MB=OM，OE=ON，ND=NP．

    （1）b=　　；

    （2）求证：四边形BCDE是平行四边形；

    （3）在直线y=﹣x+b上是否存在这样的点P，使四边形BCDE为正方形？若存在，请求出所有符合的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读与应用：

    阅读1：a、b为实数，且a＞0，b＞0，因为，所以，从而（当a＝b时取等号）．

    阅读2：函数（常数m＞0，x＞0），由阅读1结论可知： ，所以当即时，函数的最小值为．

    阅读理解上述内容，解答下列问题：

    问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为，周长为，求当x＝__________时，周长的最小值为__________．

    问题2：已知函数y1＝x＋1（x＞－1）与函数y2＝x2＋2x＋17（x＞－1），当x＝__________时， 的最小值为__________．

    问题3：某民办学习每天的支出总费用包含以下三个部分：一是教职工工资6400元；二是学生生活费每人10元；三是其他费用．其中，其他费用与学生人数的平方成正比，比例系数为0.01．当学校学生人数为多少时，该校每天生均投入最低？最低费用是多少元？（生均投入＝支出总费用÷学生人数）

    查看答案和解析>>

    同步练习册答案