
”¾ĢāÄæ”æÄ³Ń§Š£ŌŚŅßĒéĘŚ¼äĄūÓĆĶųĀē×éÖÆĮĖŅ»“Ī·Ą”°ŠĀ¹Ś²”¶¾”±ÖŖŹ¶¾ŗČü£¬ĘĄ³öĢŲµČ½±10ČĖ£¬ÓÅŠć½±20ČĖ£®Ń§Š£¾ö¶ØøųĖłÓŠ»ń½±Ń§Éśø÷·¢Ņ»·Ż½±Ę·£¬Ķ¬Ņ»µČ“ĪµÄ½±Ę·ĻąĶ¬£®
£Ø1£©£ØĮŠ·½³Ģ×é½āÓ¦ÓĆĢā£©ČōĢŲµČ½±ŗĶÓÅŠć½±µÄ½±Ę··Ö±šŹĒæŚÕÖŗĶĪĀ¶Č¼Ę£¬æŚÕÖµ„¼ŪµÄ2±¶ÓėĪĀ¶Č¼Ęµ„¼ŪµÄ3±¶ĻąµČ£¬¹ŗĀņÕāĮ½ÖÖ½±Ę·Ņ»¹²»Ø·Ń700ŌŖ£¬ĒóæŚÕÖŗĶĪĀ¶Č¼ĘµÄµ„¼Ūø÷ŹĒ¶ąÉŁŌŖ£æ
£Ø2£©£ØĄūÓĆ²»µČŹ½»ņ²»µČŹ½×é½āÓ¦ÓĆĢā£©ČōĮ½ÖÖ½±Ę·µÄµ„¼Ū¶¼ŹĒÕūŹż£¬ĒŅŅŖĒóĢŲµČ½±µ„¼Ū±ČÓÅŠć½±µ„¼Ū¶ą20ŌŖ£®ŌŚ×Ü·ŃÓĆ²»ÉŁÓŚ440¶ųÉŁÓŚ500ŌŖµÄĒ°ĢįĻĀ£¬¹ŗĀņÕāĮ½ÖÖ½±Ę·Ź±ĖüĆĒµÄµ„¼ŪÓŠ¼øÖÖĒéæö£¬Ēė·Ö±šĒó³öĆæÖÖĒéæöĢŲµČ½±ŗĶÓÅŠć½±½±Ę·µÄµ„¼Ū£®
”¾“š°ø”æ£Ø1£©æŚÕֵĵ„¼ŪŹĒ30ŌŖ£¬ĪĀ¶Č¼ĘµÄµ„¼ŪŹĒ20ŌŖ£»£Ø2£©¹ŗĀņĮ½ÖÖ½±Ę·Ź±ĖüĆĒµÄµ„¼ŪÓŠĖüĆĒµÄµ„¼ŪÓŠĮ½ÖÖĒéæö£ŗµŚŅ»ÖÖĒéæöÖŠ£ŗÓÅŠć½±µ„¼ŪĪŖ8ŌŖ£¬ĢŲµČ½±µÄµ„¼ŪĪŖ28ŌŖ£»µŚ¶žÖÖĒéæöÖŠ£ŗÓÅŠć½±µ„¼ŪĪŖ9ŌŖ£¬ŌņĢŲµČ½±µÄµ„¼ŪĪŖ29ŌŖ
”¾½āĪö”æ
£Ø1£©±¾ĢāæÉÉčæŚÕֵĵ„¼ŪŹĒyŌŖ£¬ĪĀ¶Č¼ĘµÄµ„¼ŪŹĒzŌŖ£¬Č»ŗóøł¾ŻĢāŅā£¬ÓɵČĮæ¹ŲĻµ£ŗæŚÕÖµ„¼ŪµÄ2±¶ÓėĪĀ¶Č¼Ęµ„¼ŪµÄ3±¶ĻąµČ£»¹ŗĀņÕāĮ½ÖÖ½±Ę·Ņ»¹²»Ø·Ń700ŌŖĮŠ³ö·½³Ģ×飬»Æ¼ņ¼“æÉµĆ³ö“š°ø£®
£Ø2£©±¾ĢāæÉÉčÓÅŠć½±µ„¼ŪĪŖxŌŖ£¬ŌņĢŲµČ½±µÄµ„¼ŪĪŖ£Øx+20£©ŌŖ£¬ŌŁøł¾ŻĢāŅāÕŅµ½²»µČŹ½¹ŲĻµ£ŗ×Ü·ŃÓĆ²»ÉŁÓŚ440¶ųÉŁÓŚ500ŌŖ£¬ĮŠ³ö²»µČŹ½×飬½ā²»µČŹ½×鼓æÉĒó½ā£®
½ā£ŗ£Ø1£©ÉčæŚÕֵĵ„¼ŪŹĒyŌŖ£¬ĪĀ¶Č¼ĘµÄµ„¼ŪŹĒzŌŖ£¬
øł¾ŻĢāŅāµĆ![]() £¬
£¬
½āµĆ![]() £®
£®
“š£ŗæŚÕֵĵ„¼ŪŹĒ30ŌŖ£¬ĪĀ¶Č¼ĘµÄµ„¼ŪŹĒ20ŌŖ£®
£Ø2£©ÉčÓÅŠć½±µ„¼ŪĪŖxŌŖ£¬ŌņĢŲµČ½±µÄµ„¼ŪĪŖ£Øx+20£©ŌŖ£®
øł¾ŻĢāŅāµĆ440”Ü10£Øx+20£©+20x£¼500£¬
½āµĆ8”Üx£¼10£®
ŅņĪŖĮ½ÖÖ½±Ę·µÄµ„¼Ū¶¼ŹĒÕūŹż£¬
ĖłŅŌx£½8»ņx£½9£®
µ±x£½8Ź±£¬x+20£½28£»
µ±x£½9Ź±£¬x+20£½29£®
“š£ŗ¹ŗĀņĮ½ÖÖ½±Ę·Ź±ĖüĆĒµÄµ„¼ŪÓŠĖüĆĒµÄµ„¼ŪÓŠĮ½ÖÖĒéæö£ŗ
µŚŅ»ÖÖĒéæöÖŠ£ŗÓÅŠć½±µ„¼ŪĪŖ8ŌŖ£¬ĢŲµČ½±µÄµ„¼ŪĪŖ28ŌŖ£»
µŚ¶žÖÖĒéæöÖŠ£ŗÓÅŠć½±µ„¼ŪĪŖ9ŌŖ£¬ŌņĢŲµČ½±µÄµ„¼ŪĪŖ29ŌŖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»øö°ė¾¶ĪŖrµÄŌ²ŠĪÖ½Ę¬ŌŚ±ß³¤ĪŖa£Ø ![]() £©µÄµČ±ßČż½ĒŠĪÄŚČĪŅāŌĖ¶Æ£¬ŌņŌŚøƵȱßČż½ĒŠĪÄŚ£¬ÕāøöŌ²ŠĪÖ½Ę¬”°²»Äܽӓ„µ½µÄ²æ·Ö”±µÄĆ껿ŹĒ£Ø £©
£©µÄµČ±ßČż½ĒŠĪÄŚČĪŅāŌĖ¶Æ£¬ŌņŌŚøƵȱßČż½ĒŠĪÄŚ£¬ÕāøöŌ²ŠĪÖ½Ę¬”°²»Äܽӓ„µ½µÄ²æ·Ö”±µÄĆ껿ŹĒ£Ø £©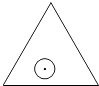
A.![]()
B.![]()
C.![]()
D.¦Šr2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĖ®¹ūµź¼Ę»®½ųA£¬BĮ½ÖÖĖ®¹ū¹²140Ē§æĖ£¬ÕāĮ½ÖÖĖ®¹ūµÄ½ų¼ŪŗĶŹŪ¼ŪČē±ķĖłŹ¾
½ų¼Ū | ŹŪ¼Ū | |
AÖÖĖ®¹ū | 5 | 8 |
BÖÖĖ®¹ū | 9 | 13 |
![]() ČōøĆĖ®¹ūµź¹ŗ½ųÕāĮ½ÖÖĖ®¹ū¹²»Ø·Ń1020ŌŖ£¬ĒóøĆĖ®¹ūµź·Ö±š¹ŗ½ųA£¬BĮ½ÖÖĖ®¹ūø÷¶ąÉŁĒ§æĖ£æ
ČōøĆĖ®¹ūµź¹ŗ½ųÕāĮ½ÖÖĖ®¹ū¹²»Ø·Ń1020ŌŖ£¬ĒóøĆĖ®¹ūµź·Ö±š¹ŗ½ųA£¬BĮ½ÖÖĖ®¹ūø÷¶ąÉŁĒ§æĖ£æ
![]() ŌŚ
ŌŚ![]() µÄ»ł“”ÉĻ£¬ĪŖĮĖÓ½Ó“ŗ½ŚµÄĄ“ĮŁ£¬Ė®¹ūµźĄĻ°å¾ö¶Ø°ŃAÖÖĖ®¹ūČ«²æ°ĖÕŪ³öŹŪ£¬BÖÖĖ®¹ūČ«²æ½µ¼Ū
µÄ»ł“”ÉĻ£¬ĪŖĮĖÓ½Ó“ŗ½ŚµÄĄ“ĮŁ£¬Ė®¹ūµźĄĻ°å¾ö¶Ø°ŃAÖÖĖ®¹ūČ«²æ°ĖÕŪ³öŹŪ£¬BÖÖĖ®¹ūČ«²æ½µ¼Ū![]() ³öŹŪ£¬ÄĒĆ“ŹŪĶźŗó¹²»ńĄū¶ąÉŁŌŖ£æ
³öŹŪ£¬ÄĒĆ“ŹŪĶźŗó¹²»ńĄū¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŌOAĪŖ±ßµÄ”÷OABĆ껿ĪŖ2£¬ĘäÖŠµćBµÄŗį”¢×Ż×ų±ź¾ł²»³¬¹ż4£¬ĒŅ¶¼²»Š”ÓŚ0£¬ŌŚĻĀĮŠŠšŹöÖŠ£¬ÕżČ·µÄŹĒ£ŗ_____£®£ØĒėŠ“³öĖłÓŠÕżČ·µÄŃ”Ļī£©
¢ŁČōµćBµÄŗį×ų±źŹĒ4£¬ŌņĀś×ćĢõ¼žµÄµćBÓŠĒŅÖ»ÓŠ1øö£»
¢ŚČōµćBŹĒÕūµć£Ø¼“ŗį”¢×Ż×ų±ź¶¼ŹĒÕūŹż£©£¬ŌņĀś×ćĢõ¼žµÄµćBÓŠ4øö£»
¢ŪŌŚ×ų±źĻµÄŚ£¬¶ŌÓŚČĪŅāĀś×ćĢāŅāµÄµćB£¬Ņ»¶Ø“ęŌŚŅ»µćC£¬Ź¹µĆ”÷CAB”¢”÷COA”¢”÷COBĆ껿ĻąµČ£»
¢ÜŌŚ×ų±źĻµÄŚ£¬“ęŌŚŅ»øö¶ØµćD£¬Ź¹µĆ¶ŌÓŚČĪŅāĀś×ćĢõ¼žµÄµćB£¬”÷DBA”¢”÷DBOĆ껿ĻąµČ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģx2©£Øm+1£©x+ ![]() £Øm2+1£©=0ÓŠŹµŹżøł£®
£Øm2+1£©=0ÓŠŹµŹżøł£®
£Ø1£©ĒómµÄÖµ£»
£Ø2£©ĻČ×÷y=x2©£Øm+1£©x+ ![]() £Øm2+1£©µÄĶ¼Ļó¹ŲÓŚxÖįµÄ¶Ō³ĘĶ¼ŠĪ£¬Č»ŗó½«Ėł×÷Ķ¼ŠĪĻņ×óĘ½ŅĘ3øöµ„Ī»³¤¶Č£¬ŌŁĻņÉĻĘ½ŅĘ2øöµ„Ī»³¤¶Č£¬Š“³ö±ä»ÆŗóĶ¼ĻóµÄ½āĪöŹ½£»
£Øm2+1£©µÄĶ¼Ļó¹ŲÓŚxÖįµÄ¶Ō³ĘĶ¼ŠĪ£¬Č»ŗó½«Ėł×÷Ķ¼ŠĪĻņ×óĘ½ŅĘ3øöµ„Ī»³¤¶Č£¬ŌŁĻņÉĻĘ½ŅĘ2øöµ„Ī»³¤¶Č£¬Š“³ö±ä»ÆŗóĶ¼ĻóµÄ½āĪöŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µ±Ö±Ļßy=2x+n£Øn”Żm£©Óė±ä»ÆŗóµÄĶ¼ĻóÓŠ¹«¹²µćŹ±£¬Ēón2©4nµÄ×ī“óÖµŗĶ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļß![]() Óė
Óė![]() Öį”¢
Öį”¢![]() Öį·Ö±š½»ÓŚ
Öį·Ö±š½»ÓŚ![]() ”¢
”¢![]() Į½µć£¬ŌŚ
Į½µć£¬ŌŚ![]() ÖįÉĻÓŠŅ»µć
ÖįÉĻÓŠŅ»µć![]() £¬¶Æµć
£¬¶Æµć![]() “Ó
“Ó![]() µćŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲ
µćŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲ![]() ÖįĻņ×óŅĘ¶Æ£®
ÖįĻņ×óŅĘ¶Æ£®
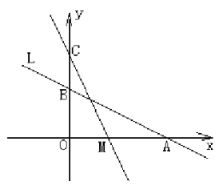
£Ø1£©Ēó![]() ”¢
”¢![]() Į½µćµÄ×ų±ź
Į½µćµÄ×ų±ź
£Ø2£©Ēó![]() µÄĆ껿
µÄĆ껿![]() Óė
Óė![]() µÄŅĘ¶ÆŹ±¼ä
µÄŅĘ¶ÆŹ±¼ä![]() £ØĆė£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£ØĆė£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©µ±![]() ŗĪÖµŹ±
ŗĪÖµŹ±![]() £¬²¢Ēó“ĖŹ±
£¬²¢Ēó“ĖŹ±![]() µćµÄ×ų±ź£®
µćµÄ×ų±ź£®
£Ø4£©µ±![]() ŗĪÖµŹ±
ŗĪÖµŹ±![]() µÄĆ껿ŹĒ
µÄĆ껿ŹĒ![]() Ņ»°ė£¬²¢Ēó“ĖŹ±
Ņ»°ė£¬²¢Ēó“ĖŹ±![]() µćµÄ×ų±ź£®
µćµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶CDŹĒĻŅ£¬ČōAB=10cm£¬CD=8cm£¬ÄĒĆ“A”¢BĮ½µćµ½Ö±ĻßCDµÄ¾ąĄėÖ®ŗĶĪŖ cm.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒÓÉ”°ÕŌĖ¬ĻŅĶ¼”±±ä»ÆµĆµ½µÄ£¬ĖüÓÉ°ĖøöČ«µČµÄÖ±½ĒČż½ĒŠĪĘ“½Ó¶ų³É£¬¼ĒĶ¼ÖŠÕż·½ŠĪABCD£¬Õż·½ŠĪEFGH£¬Õż·½ŠĪMNKTµÄĆ껿·Ö±šĪŖ![]() ,Čō
,Čō![]() £¬Ōņ
£¬Ōņ![]() µÄÖµŹĒ_______£®
µÄÖµŹĒ_______£®
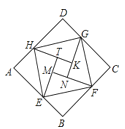
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶź³ÉĻĀĆęµÄÖ¤Ć÷¹ż³Ģ£ŗ
ČēĶ¼ĖłŹ¾£¬Ö±ĻßADÓėAB£¬CD·Ö±šĻą½»ÓŚµćA£¬D£¬ÓėEC£¬BF·Ö±šĻą½»ÓŚµćH£¬G£¬ŅŃÖŖ”Ļ1£½”Ļ2£¬”ĻB£½”ĻC£®
ĒóÖ¤£ŗ”ĻA£½”ĻD£®
Ö¤Ć÷£ŗ”ß”Ļ1£½”Ļ2£¬£ØŅŃÖŖ£©”Ļ2£½”ĻAGB£Ø”” ””£©
”ą”Ļ1£½”” ””£Ø”” ””£©
”ąEC”ĪBF£Ø”” ””£©
”ą”ĻB£½”ĻAEC£Ø”” ””£©
Ó֔ߔĻB£½”ĻC£ØŅŃÖŖ£©
”ą”ĻAEC£½”” ””£Ø”” ””£©
”ą”” ””£Ø”” ””£©
”ą”ĻA£½”ĻD£Ø”” ””£©

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com