
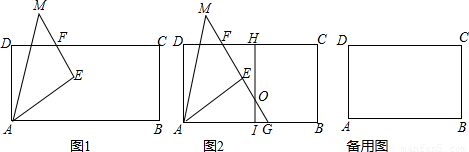
 AB=12,在Rt△AEQ中,运用勾股定理得出EQ=5,则PE=8,再设DF=x,在Rt△PEF中,运用勾股定理列出关于x的方程,解方程即可;②当EC=BC=13时,连接AC.由AE+EC=13+13<AC=
AB=12,在Rt△AEQ中,运用勾股定理得出EQ=5,则PE=8,再设DF=x,在Rt△PEF中,运用勾股定理列出关于x的方程,解方程即可;②当EC=BC=13时,连接AC.由AE+EC=13+13<AC= ,根据三角形两边之和大于第三边得出△AEC不存在,即不可能出现EC=BC;③当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,先由EC=EB,得出E在BC的垂直平分线上,则PE=EQ=
,根据三角形两边之和大于第三边得出△AEC不存在,即不可能出现EC=BC;③当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,先由EC=EB,得出E在BC的垂直平分线上,则PE=EQ=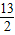 ,再解Rt△AQE,得到∠EAQ=30°,由同角的余角相等得出∠PEF=30°,然后解Rt△PEF即可;
,再解Rt△AQE,得到∠EAQ=30°,由同角的余角相等得出∠PEF=30°,然后解Rt△PEF即可; 解:(1)线段DF与EF相等,理由如下:
解:(1)线段DF与EF相等,理由如下: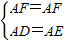 ,
,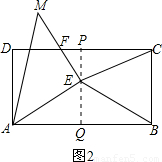 (2)分三种情况:
(2)分三种情况: AB=12.
AB=12.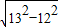 =5,
=5,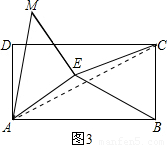 即82+(12-x)2=x2,
即82+(12-x)2=x2,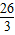 ,
,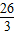 ;
; =
= ,
, ,
,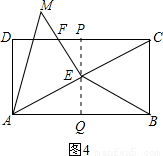 ③如图3,当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,则PQ⊥AB,AQPD是矩形.
③如图3,当EC=EB时,过E作EP⊥CD于P,延长PE交AB于Q,则PQ⊥AB,AQPD是矩形.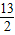 .
. AE,∠AQE=90°,
AE,∠AQE=90°,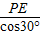 =
=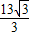 ,
,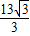 ;
;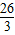 或
或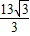 ;
;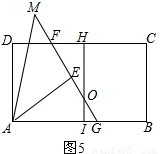 (3)如图5,同(1)可证OE=OI,
(3)如图5,同(1)可证OE=OI,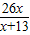 .
.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com