
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘除运算,再计算加减运算即可得到结果;
(3)原式利用乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.
解答 解:(1)原式=($\frac{1}{4}$+2$\frac{3}{4}$)+(-2$\frac{1}{3}$-3$\frac{2}{3}$)=3-6=-3;
(2)原式=42×$\frac{7}{6}$+24×5=49+120=169;
(3)原式=-18+27-14=-5;
(4)原式=-8×25-2+100=-102.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
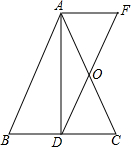 如图,已知在△ABC中,D为BC上一点,连接AD,过点A作AF∥BC,过点D作DF∥AB,AF与DF交于点F,DF与AC交于点O,若AO=OC.
如图,已知在△ABC中,D为BC上一点,连接AD,过点A作AF∥BC,过点D作DF∥AB,AF与DF交于点F,DF与AC交于点O,若AO=OC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | ∠B=2∠K | |
| B. | 六边形ABCDEF的周长=六边形GHIJKL的周长 | |
| C. | BC=2HI | |
| D. | S六边形ABCDEF=2S六边形GHIJKL |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com