
【题目】(9分)已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.


(1)(4分)求证:△AOD≌△EOC;
(2)(5分)连接AC,DE,当∠B=∠AEB= °时,四边形ACED是正方形?请说明理由.
【答案】(1)证明见试题解析;(2)45,理由见试题解析.
【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法(ASA),得出△AOD≌△EOC;
(2)利用等腰直角三角形的性质结合平行四边形的判定以及正方形的判定得出即可.
试题解析:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADC=∠DCE,在△AOD和△EOC中,∵∠ADO=∠ECO,DO=CO,∠DOA=∠EOC,∴△AOD≌△EOC(ASA);
(2)当∠B=∠AEB=45°时,四边形ACED是正方形,理由:∵∠B=∠AEB=45°,∴AB=AE,∵△AOD≌△EOC,∴AD=EC,∠DAE=∠AEC=45°,又∵AD∥EC,∴四边形ACED是平行四边形,则AD=BC=EC,∴AC⊥EC,∵△ABE是等腰直角三角形,∴AC=EC,∠ACE=90°,∴平行四边形ACED是正方形.故答案为:45°.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
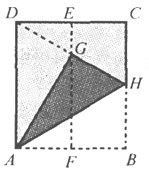
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
A. 2cm B. ![]() cm C. 4cm D.
cm C. 4cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元前6世纪古希腊的毕达哥拉斯学派有一种观点,即“万物皆数”,一切量都可以用整数或整数比(分数)表示,后来,当这一学派中的希帕索斯发现,边长为1的正方形的对角线的长度不能用整数或整数的比表示时,毕达哥拉斯学派感到惊恐不安,由此,引发了第一次数学危机,这儿“不能用整数或整数的比表示的数”指的是( )
A.有理数B.无理数C.合数D.质数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算“△”:对于任意实数a,b且a≥b时,都有a△b=a2﹣ab+b2 , 如5△4=52﹣5×4+42=21,若(x﹣3)△4=21,则实数x的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
(1)求证:点E是![]() 的中点;
的中点;
(2)当BC=12,且AD:CD=1:2时,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com