
【题目】如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,则∠BOC= °,∠DOE= °;
(2)若∠AOC=m°,∠AOB=n°(n>m),则∠BOC= °,∠DOE= °;
(3)猜想:∠DOE与∠BOC有怎样的数量关系?并说明理由.

【答案】(1)90,45;(2)(n﹣m),![]() (n﹣m);(3)∠DOE=
(n﹣m);(3)∠DOE=![]() ∠BOC.
∠BOC.
【解析】
(1) 依据∠AOC=20°, ∠AOB=110°, 可得∠BOC=110° -20°=90°; 再根据OD、 OE分别平分∠AOB, ∠AOC, 即可得到∠DOE的度数;
(2) 依据∠AOC= m°, ∠AOB= n°,可得∠BOC= n°- m°= (n°- m°); 再根据OD、 OE分别平分∠AOB、 ∠AOC, 可得∠AOD= ![]() n°, LAOE=
n°, LAOE= ![]() m°,进而得出∠DOE的度数;
m°,进而得出∠DOE的度数;
(3) 依据OD、 OE分别平分∠AOB、 ∠AOC, 即可得出∠AOD=![]() ∠AOB, ∠AOE=
∠AOB, ∠AOE=![]() ∠AOC, 进而得到∠DOE=∠AOD-∠AOE=
∠AOC, 进而得到∠DOE=∠AOD-∠AOE= ![]() (∠AOB-∠AOC) =
(∠AOB-∠AOC) =![]() ∠BOC.
∠BOC.
解:(1)
∵∠AOC=20°,∠AOB=110°,
∴∠BOC=110°﹣20°=90°;
∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=55°,∠AOE=10°,
∴∠DOE=55°﹣10°=45°;
故答案为:90,45;
(2)∵∠AOC=m°,∠AOB=n°,
∴∠BOC=n°﹣m°=(n﹣m)°;
∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=![]() n°,∠AOE=
n°,∠AOE=![]() m°,
m°,
∴∠DOE=∠AOD﹣∠AOE=![]() (n﹣m)°;
(n﹣m)°;
故答案为:(n﹣m),![]() (n﹣m);
(n﹣m);
(3)∠DOE=![]() ∠BOC.
∠BOC.
证明:∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=![]() ∠AOB,∠AOE=∠AOC,
∠AOB,∠AOE=∠AOC,
∴∠DOE=∠AOD﹣∠AOE=![]() (∠AOB﹣∠AOC)=
(∠AOB﹣∠AOC)=![]() ∠BOC.
∠BOC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为( ![]() ,0)、(3
,0)、(3 ![]() ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
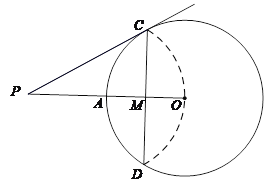
【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
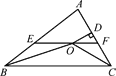
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB. 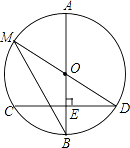
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:
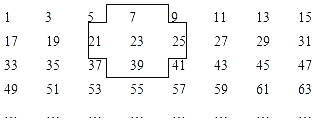
(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.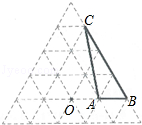
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
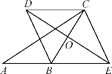
【题目】已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com