
【题目】在△ABC 中,AE、BF 是角平分线,交于 O 点.
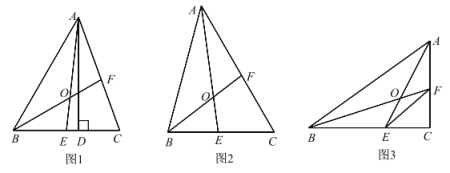
(1)如图 1,AD 是高,∠BAC=90°,∠C=70°,求∠DAC 和∠BOA 的度数;
(2)如图 2,若 OE=OF,求∠C 的度数;
(3)如图 3,若∠C=90°,BC=8,AC=6,S△CEF=4,求 S△AOB.
【答案】(1)∠DAC=20°,∠BOA=125° (2)60° (3)10
【解析】
(1)根据垂直的定义得到∠ADC=90°,根据角平分线的定义得到∠ABO=30°,根据三角形的内角和即可得到结论;
(2)连接OC,根据角平分线的性质得到OM=ON,根据全等三角形的性质得到∠EOM=∠FOH,根据角平分线的定义即可得到结论;
(3)根据勾股定理得到AB=![]() =10,根据三角形的面积公式得到CF,求得AF,得到S△ABF=S△ABC-S△BCF,根据角平分线定理得到
=10,根据三角形的面积公式得到CF,求得AF,得到S△ABF=S△ABC-S△BCF,根据角平分线定理得到![]() ,求得
,求得![]() =3,于是得到结论.
=3,于是得到结论.
(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°-90°-70°=20°;
∵∠BAC=50°,∠C=70°,
∴∠BAO=25°,∠ABC=60°,
∵BF是∠ABC的角平分线,
∴∠ABO=30°,
∴∠BOA=180°-∠BAO-∠ABO=180°-25°-30°=125°;
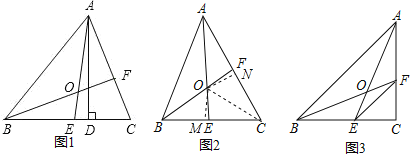
(2)如图2:连接OC,
∴AE、BF是角平分线,交于O点,
∴OC是∠ACB的角平分线,
∴∠OCF=∠OCE,
过O作OM⊥BC,ON⊥AC,
则OM=ON,
在Rt△OEM与Rt△OFN中,
![]() ,
,
∴Rt△OEM≌Rt△OFN,(HL),
∴∠EOM=∠FON,
∴∠MON=∠EOF=180°-∠C,
∵AE、BF是角平分线,
∴∠AOB=90°+![]() ∠ACB,
∠ACB,
即90°+![]() ∠ACB=180°-∠ACB,
∠ACB=180°-∠ACB,
∴∠ACB=60°;
(3)∵∠C=90°,BC=8,AC=6,
∴AB=![]() =10,
=10,
∵AE是角平分线,
∴![]() ,
,
∴BE=5,CE=3,
∵S△CEF=![]() ECCF=
ECCF=![]() ×3CF=4,
×3CF=4,
∴CF=![]() ,
,
∴AF=![]() ,
,
∵S△ABC=![]() BCAC=
BCAC=![]() ×8×6=24,
×8×6=24,
∴S△ABF=S△ABC-S△BCF=24-![]() ×8×
×8×![]() =
=![]()
∵AE平分∠BAC,
∴![]()
∴![]() =3,
=3,
∴![]()
∴S△AOB=![]() =10.
=10.


科目:初中数学 来源: 题型:
【题目】八年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成A,B,C,D,E五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
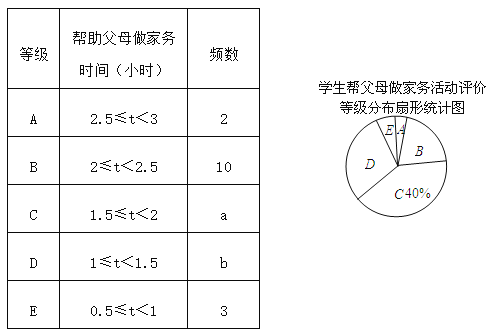
(1)求a,b的值;
(2)根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.

有以下结论:
①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
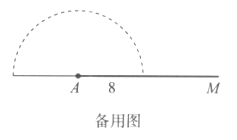
其中所有正确结论的序号是( )
A.②③B.③④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一抛物线与x轴的交点是A(﹣2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式,并写出顶点坐标.
(2)直接写出当y>8时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,边AB与y轴交于点C.

(1)若∠A=∠AOC,试说明:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地教育局为了解该地八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:
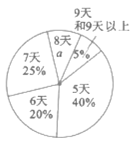

请根据图中提供的信息,回答下列问题:
(1)![]() ___________,并写出该扇形所对圆心角的度数为___________,请补全条形统计图.
___________,并写出该扇形所对圆心角的度数为___________,请补全条形统计图.
(2)在这次抽样调查中,众数为___________,中位数为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com