
����Ŀ������ͼ����̽���������������зdz���Ҫ�����ã��������Ǿ�һ������ĺ���չ��̽����������![]() ��ͼ������������ʽ���б�����㡢���߹��̵õ�����ͼ������ͼ��ʾ��
��ͼ������������ʽ���б�����㡢���߹��̵õ�����ͼ������ͼ��ʾ��
| ���� | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ���� |
| ���� | 6 | 4 | 2 | 0 | 2 | 4 | 6 | ���� |
����ͬ���Ĺ��̻�����![]() ��
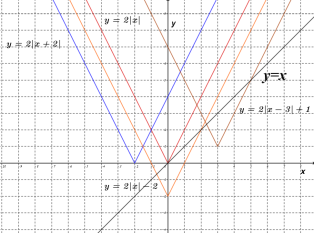
��![]() ��ͼ������ͼ��ʾ���۲췢�֣�����������ͼ����������������ɵ���Գ�ͼ�Σ�������������ʽ�о���ֵǰ���ϵ����ͬ����ͼ��Ŀ��ڷ������״��ȫ��ͬ��ֻ����ߵ�ͶԳ��ᷢ���˱仯��
��ͼ������ͼ��ʾ���۲췢�֣�����������ͼ����������������ɵ���Գ�ͼ�Σ�������������ʽ�о���ֵǰ���ϵ����ͬ����ͼ��Ŀ��ڷ������״��ȫ��ͬ��ֻ����ߵ�ͶԳ��ᷢ���˱仯��
![]() ��ֱ��д��
��ֱ��д��![]() ��
��![]() �Ľ�������ͺ���
�Ľ�������ͺ���![]() �ĶԳ��
�ĶԳ��
![]() ��������ƽ��ֱ������ϵ�ڻ�������
��������ƽ��ֱ������ϵ�ڻ�������![]() ��ͼ��(���б�)����д������
��ͼ��(���б�)����д������![]() ��һ�����ʣ�
��һ�����ʣ�
![]() ��Ϻ���ͼ��ֱ��д������ʽ
��Ϻ���ͼ��ֱ��д������ʽ![]() ʱ
ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��

���𰸡���1����������Ϊ����1��2�����Գ���Ϊֱ��x����2����2��ͼ������������ʣ�����![]() ��ͼ��ĶԳ���Ϊֱ��x��3���𰸲�Ψһ������3��
��ͼ��ĶԳ���Ϊֱ��x��3���𰸲�Ψһ������3��![]()
��������
��1����������ͼ�ɵõ��𰸣�
��2����������![]() ��ͼ�������ͼ�ɵõ���Ӧ��ͼ�����ʣ�
��ͼ�������ͼ�ɵõ���Ӧ��ͼ�����ʣ�
��3���Ȼ���![]() �ĺ���ͼ����ͨ����
�ĺ���ͼ����ͨ����![]() ������������������꣬��Ϻ���ͼ�ɵõ��𰸣�
������������������꣬��Ϻ���ͼ�ɵõ��𰸣�
�⣺��1����ͼ���֪��![]() ��
��![]() �Ľ�������Ϊ����1��2����
�Ľ�������Ϊ����1��2����
����![]() �ĶԳ���Ϊֱ��x����2��
�ĶԳ���Ϊֱ��x����2��
��2������![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��

���ʣ�����![]() ��ͼ��ĶԳ���Ϊֱ��x��3���𰸲�Ψһ����
��ͼ��ĶԳ���Ϊֱ��x��3���𰸲�Ψһ����
��3������![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
���![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��һ����������Ϊ��5��5����
��һ����������Ϊ��5��5����
��![]() ʱ��
ʱ��![]() ��
��
���![]() ��
��
��![]() ��
��
��![]() ��
��![]() ����һ����������Ϊ��
����һ����������Ϊ��![]() ��
��![]() ����
����
����ͼ���֪������ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD��������A��AE��BC������ΪE������DE��FΪ�߶�DE��һ��������AFE=��B��
��1����֤����ADF�ס�DEC��
��2����AB=8��AD=![]() ��AF=
��AF=![]() ����AE�ij���
����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=3����B=50�㣬��D��BC���ϣ������B��C�غϣ�������AD������ADE=50�㣬DE����AC�ڵ�E.
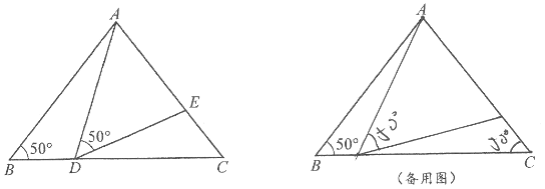
��1������BAD=20��ʱ�����CDE�Ķ�����
��2����CD���ڶ���ʱ����ABD�ա�DCE��Ϊʲô��
��3���ڵ�D�˶��Ĺ����У���ADE�����ǵ����������������ܣ�ֱ��д����DAE�Ķ������������ܣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ķ�������ϣ����б��A��B��C��3��С��������ǿյأ�����6��С��������Dz�ƺ����������С���������ȫ��ͬ��

��1��һֻ���ɷ��е������������ͼ�еķ�������ϣ���С�����ڲ�ƺ�ϵĸ����Ƕ��٣�
��2���ִ�3��С����յ�������ѡȡ2����ֲ��ƺ����պ�ѡȡA��B��2��С����յ���ֲ��ƺ�ĸ����Ƕ��٣�������ͼ���б�����⣩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������3 000Ԫ����ij�ָɹ����ۣ���������״�����ã������ֵ���9 000Ԫ�������ָɹ�������εĽ��۱ȵ�һ�εĽ��������20%�������ɹ������ȵ�һ�ε�2������300 kg.������а�9Ԫ/kg�ļ۸���ۣ����ָɹ��۳������µ�600 kg���ۼ۵İ������꣮
(1)���ָɹ���һ�εĽ����Ƕ��٣�
(2)�����������ָɹ���ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��BDΪ��O��ֱ����BD��AC�ཻ�ڵ�H��AC���ӳ��������B��ֱ���ཻ�ڵ�E���ҡ�A=��EBC��
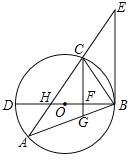
��1����֤��BE�ǡ�O�����ߣ�
��2����֪CG��EB����CG��BD��BA�ֱ��ཻ�ڵ�F��G����BGBA=48��FG=![]() ��DF=2BF����AH��ֵ��
��DF=2BF����AH��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��50Ԫ���ۼ�Ϊÿ��60Ԫ��ÿ�������190�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ������10������ÿ����Ʒ���ۼ�����xԪ��ÿ�����������ΪyԪ��
��1����y����x�Ĺ�ϵʽ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ�������ǡΪ1980Ԫ��
��3��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ��ɻ�����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB=4��BC=3��������ֱ�����������½ǵĶ���B������ת90����ͼ��λ�ã��������½ǵĶ������������ת90����ͼ��λ�ã������Դ����ƣ�����������ת2016�κ���A��������ת��������������·��֮���ǣ�������

A. 2015�� B. 3019.5�� C. 3018�� D. 3024��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A����4��2����B��n����4��������һ�κ���y=kx+b�ͷ���������y=![]() ͼ����������㣮
ͼ����������㣮
��1����һ�κ����ͷ����������Ľ���ʽ��
��2������AOB�������
��3���۲�ͼ��ֱ��д������ʽkx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com