
 如图,AC=AE,∠1=∠2,AB=AD,求证:∠B=∠D.
如图,AC=AE,∠1=∠2,AB=AD,求证:∠B=∠D. 科目:初中数学 来源: 题型:解答题
 如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.
如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中∠A=90°,甲、乙二人从点D同时出发,甲沿DA,AB过桥到达点B处,乙沿DC过桥由点C直达B处.已知DA=6千米,AB=6千米,DC=2千米,假设甲、乙两人的速度相同,问:甲、乙二人谁先到达B处?说明理由.
如图,在Rt△ABC中∠A=90°,甲、乙二人从点D同时出发,甲沿DA,AB过桥到达点B处,乙沿DC过桥由点C直达B处.已知DA=6千米,AB=6千米,DC=2千米,假设甲、乙两人的速度相同,问:甲、乙二人谁先到达B处?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
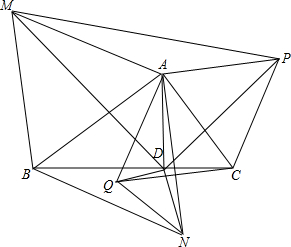 AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.
AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
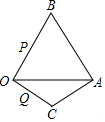 已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题:
已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com