
 如图,点M是正方形ABCD的边CD的中点,正方形ABCD的边长为4cm,点P按A→B→C→M的顺序在正方形的边上以每秒2cm的速度作匀速运动,设点P的运动时间为x(秒),△APM的面积为y(cm2)
如图,点M是正方形ABCD的边CD的中点,正方形ABCD的边长为4cm,点P按A→B→C→M的顺序在正方形的边上以每秒2cm的速度作匀速运动,设点P的运动时间为x(秒),△APM的面积为y(cm2)分析 (1)先求出AB=BC=CD=AD=4,进而求出AP=2×1=2cm,再用三角形的面积得出S△AMP=$\frac{1}{2}$AP•AD=4;
(2)先判断出点P在边BC上,由运动知,BP=2x-4,CP=8-2x,再求出DM=CM=2,最后利用面积的差即可得出结论;
(3)分三种情况,利用三角形的面积公式即可.
解答 解:(1)如图1, ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,
当点P运动1秒时,AP=2×1=2cm.
∴S△AMP=$\frac{1}{2}$AP•AD=$\frac{1}{2}$×2×4=4;
(2)当x=2时,运动的路程为2×2=4cm,当x=4时,运动路程为4×2=8,
∴当2≤x≤4时,点P在BC边上,由运动知,BP=2x-4,CP=8-2x,
∵M为CD的中点,
∴DM=CM=2,
∴y=S△AMP=S正方形ABCD-S△ADM-S△ABP-S△PCM
=AB2-$\frac{1}{2}$DM•AD-$\frac{1}{2}$AB•BP-$\frac{1}{2}$CM•CP
=16-$\frac{1}{2}$×2×4-$\frac{1}{2}$×4×(2x-4)-$\frac{1}{2}$×2×(8-2x)
=12-2x;
(3)∵y=3
当点P在AB边上时(0<x<2),如图1,AP=2x,
∴y=S△APM=$\frac{1}{2}$AP×AD=$\frac{1}{2}$×2x×4=4x=3,
∴x=$\frac{3}{4}$,
当点P在BC边上时(2≤x≤4),如题干图,由(2)知,y=12-2x=3,
∴x=$\frac{9}{2}$(不符合题意,舍)
当点P在边CM上时(4<x<5),如图2,由运动知,PM=10-2x,
∴y=S△APM=$\frac{1}{2}$PM×AD=$\frac{1}{2}$(10-2x)×4=3,
∴x=$\frac{17}{4}$,
即:满足条件的x的值为$\frac{3}{4}$或$\frac{17}{4}$.
点评 此题是四边形综合题,主要考查了正方形的性质,三角形的面积公式,解(1)的关键是求出AP,解(2)的关键是判断出点P哎边BC上,解(3)的关键是分类讨论,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
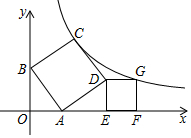 如图,正方形ABCD和正方形DEFG放置在直角坐标系中,点A,E,F在x轴的正半轴,点B在y轴的正半轴上,点C,G均在函数y=$\frac{k}{x}$的图象上,若AB=$\sqrt{3}$,则k的值是( )
如图,正方形ABCD和正方形DEFG放置在直角坐标系中,点A,E,F在x轴的正半轴,点B在y轴的正半轴上,点C,G均在函数y=$\frac{k}{x}$的图象上,若AB=$\sqrt{3}$,则k的值是( )| A. | 2$+\sqrt{2}$ | B. | 3+$\frac{3}{2}\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 3.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小李同学在求一元二次方程-2x2+4x+1=0的近似根时,先在直角坐标系中使用软件绘制了二次函数y=-2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是-1<x1<0,2<x2<3,小李同学的这种方法主要运用的数学思想是( )
小李同学在求一元二次方程-2x2+4x+1=0的近似根时,先在直角坐标系中使用软件绘制了二次函数y=-2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是-1<x1<0,2<x2<3,小李同学的这种方法主要运用的数学思想是( )| A. | 公理化 | B. | 类比思想 | C. | 数形结合 | D. | 模型思想 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com