
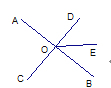
【题目】如图3,直线AB、CD相交于O,若∠AOD比∠AOC大40°,则∠BOD=___°;若∠AOD=2∠AOC,则∠BOC=___;若∠AOD=∠AOC,则∠BOD=___.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
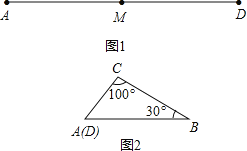
【题目】如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是( )
A. 点M在AB上
B. 点M在BC的中点处
C. 点M在BC上,且距点B较近,距点C较远
D. 点M在BC上,且距点C较近,距点B较远
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。
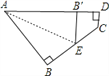
(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
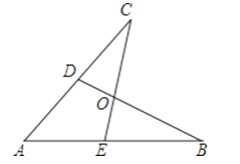
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
【答案】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC
【解析】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC;理由如下:
若AD=AE,
在△ACE和△ABD中,  ,
,
∴△ACE≌△ABD(SAS);
若CD=BE,
∵AB=AC,
∴AD=AE,
同理:△ACE≌△ABD(SAS);
若∠B=∠C,
在△ACE和△ABD中, 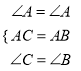 ,
,
∴△ACE≌△ABD(ASA);
若∠ADB=∠AEC,
在△ACE和△ABD中, 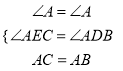 ,
,
∴△ACE≌△ABD(AAS);
故答案为:AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
点睛:本题考查了全等三角形的判定方法,是开放型题目,存在四种情况,熟练掌握全等三角形的判定方法是解决问题的关键.
【题型】填空题
【结束】
17
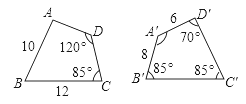
【题目】如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=________,∠A=________,B′C′=________,AD=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.

(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下调查中,应采用全面调查的是( )
A.调查某批次汽车的抗撞击能力
B.了解全国中学生的视力和用眼卫生情况
C.了解某班学生的身高情况
D.调查某池塘中现有鱼的数量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com