
分析 由已知条件得出△ABC的三边长,由勾股定理的逆定理证明△ABC是直角三角形,∠A=90°,再由三角函数的定义即可得出结果.
解答 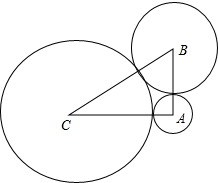 解:如图所示:
解:如图所示:
∵⊙A的半径长为1,⊙B的半径长为2,⊙C的半径长为3,且这三个圆两两外切,
∴AB=1+2=3,AC=3+1=4,BC=3+2=5,
∵AB2+AC2=BC2,
∴△ABC是直角三角形,∠A=90°,
∴cosB=$\frac{AB}{BC}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查了相切两圆的性质、勾股定理的逆定理、三角函数;熟练掌握相切两圆的性质,由勾股定理的逆定理证出三角形是直角三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )| A. | 8056 | B. | 8050 | C. | 8054 | D. | 8052 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=9,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过2秒时,直线MN和正方形AEFG开始有公共点.
如图,矩形ABCD中,AB=9,AD=3.点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的右下方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当经过2秒时,直线MN和正方形AEFG开始有公共点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )
如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在一个边长不超过8厘米的大正方形ABCD中,如图所示,放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米,那么大正方形ABCD和小正方形BEFG的边长之比为( )
在一个边长不超过8厘米的大正方形ABCD中,如图所示,放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ,已知3张小正方形纸片盖住的总面积为44平方厘米,那么大正方形ABCD和小正方形BEFG的边长之比为( )| A. | 5:3 | B. | 3:2 | C. | 10:7 | D. | 8:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).
如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com