
����Ŀ���ڱ߲���ȵ�ƽ���ı���ֽƬ����ȥһ�����Σ�����һ���ı��Σ���Ϊ��һ�β����������µ��ı���ֽƬ���ټ�ȥһ�����Σ�������һ���ı��Σ���Ϊ�ڶ��β����������������ƣ�����n�β������µ��ı��������Σ����ԭƽ���ı���Ϊn�����Σ���ͼ1����ABCD�У���AB��1��BC��2������ABCDΪ1�����Σ�
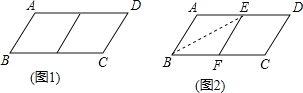
��1�����������
���ڱ߳��ֱ�Ϊ2��3��ƽ���ı����� ��������
��С��Ϊ�˼�ȥһ�����Σ��������²�������ͼ2������ABCD��BE�۵�����E��AD�ϣ���ʹ��A����BC���ϵĵ�F���õ��ı���ABFE����֤���ı���ABEF�����Σ�
��2��������̽������㣺
����֪��ABCD���ڱ߳��ֱ�Ϊ1��a��a��1��������3�����Σ��뻭����ABCD���ü��ߵ�ʾ��ͼ������ͼ���·�д��a��ֵ��
����֪��ABCD���ڱ߳��ֱ�Ϊa��b��a��b��������a��6b��r��b��5r��r��0��������ABCD
�� ��������
���𰸡���1����2���ڼ�������2���ټ���������10�����ɣ�
����Ϊa��6b��r��b��5r������a=6��5r+r=31r��b=5r����ͼ��ʾ��ƽ���ı���ABCD��10������.

�����������������
��1���������������Ķ���ش�����ƽ����+��ƽ���ߵĽṹ֤����ABE�ǵ�������������2���������������Ķ��弰���ε��ж���ͼ�����ҳ�a��b��������ϵ������ͼ��.
������1����2��
�����۵�֪����ABE=��FBE��AB=BF��
���ı���ABCD��ƽ���ı��Σ�
��AE��BF�����AEB=��FBE��
���AEB=��ABE����AE=AB��
��AE=BF��
���ı���ABFE��ƽ���ı��Σ�
���ı���ABFE�����Σ�
��2������ͼ��ʾ��

����Ϊa��6b��r��b��5r������a=6��5r+r=31r��b=5r����ͼ��ʾ��ƽ���ı���ABCD��10������.




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
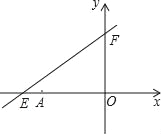
����Ŀ����ͼ��ֱ��y=kx+6��x�ᡢy��ֱ��ڵ�E��F����E������Ϊ����8��0������A������Ϊ����6��0����
��1����k��ֵ��
��2������P��x��y���ǵڶ������ڵ�ֱ���ϵ�һ�����㣬�ڵ�P���˶������У���д����OPA�����S��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3��̽�����ڣ�2��������£�����P�˶���ʲôλ��ʱ����OPA�����Ϊ![]() ����˵�����ɣ�
����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̼����ܹ�ע��С��Ϊ���˽����ǵ�ij���й���ʱʹ�ù��������������������յ��ó��жԲ��ֹ����߽��е��飬���ѵ��������Ƴ�������������ͳ��ͼ�����赱��ÿ��ÿ�ι���ʱ��ֻ��һ��������������ɽ��⣩�����Ϲ���������ɽ��⣩��

����������Ϣ���ش��������⣺
��1��С����ε��鵽�Ĺ������������������˴Σ�
��2����ȫ����ͳ��ͼ��
��3�������쵽�ó��й����߹���2000�˴Σ��������ʹ�����Ϲ�������������������˴Σ������������ �˴Σ�����C��Բ�Ľ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ����M=a+b��c��N=4a��2b+c��P=2a��b����M��N��P�У�ֵС��0�����У� �� 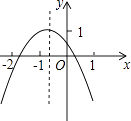
A.3��
B.2��
C.1��
D.0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽��С��ͣ���ѵ����⣬ijС�����½�50��ͣ��λ����֪�½�1������ͣ��λ��1������ͣ��λ��0.5��Ԫ���½�3������ͣ��λ��2������ͣ��λ��1.1��Ԫ��
��1����С���½�1������ͣ��λ��1������ͣ��λ���������Ԫ��
��2������ʵ���������С���½�����ͣ��λ������33������Ԥ��Ͷ�ʽ�����11��Ԫ�����м��ֽ��췽ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У����Խ���BD��һ��P����EF��BC��HG��AB�����ı���AEPH���ı���CFPG���������ΪS1��S2����S1��S2�Ĵ�С��ϵΪ��������
A��S1=S2 B��S1��S2 C��S1��S2 D������ȷ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ũ��ƻ�������������εĹ��ڣ�Ϊ�˱���ƻ�������ܷ紵������ƻ��������Χ������Ҷ��������ͼ�����Կ���ũ������ֲƻ����������(n)��ƻ������������Ҷ�������Ĺ��ɣ���nΪijһ����ֵʱ��ƻ���������������Ҷ����������nΪ(����)
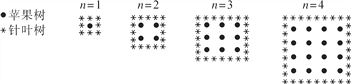
A. 6 B. 8 C. 12 D. 16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ٽ����о��õĿ��ٷ�չ���ӿ��·���裬ij���ٹ�·���蹤������������AB����ͼ����ɽ��һ��C���BC����Ϊ200m����CAB=54�㣬��CBA=30�㣬������AB�ij������ο����ݣ�sin54���0.81��cos54���0.59��tan54���1.38�� ![]() ��1.73����ȷ����λ��
��1.73����ȷ����λ�� 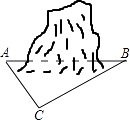
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϲ������ �����������������dz�������������������ε����⣬��ʱ���ǿ��Խ������߶εķ���������.������һ��С������ 4 ���������е�ѭ������������Ҫ�����ܵı������������Ǿ� �����ĸ��ӷֱ�Ϊ A��B��C��D���������DZ���ͬһ���߶���������ͼ��
![]()
��Ϊ��ѭ����������ÿ������֮�䶼Ҫ����һ��������൱����������ͼ�����ĸ��������߶�����һ�����ɵõ����߶��У�
AB��AC��AD��������3 ��
BC��BD������������2 ��
CD����������������1 ��
�ܵ��߶������� 3��2��1��6
���Կ�֪ 4 ���ӽ��е�ѭ����������������.
(1).��������뷨����һ��С���� 6 ���������е�ѭ�����������ܵı���������_____
(2).��������뷨����һ��С���� n ���������е�ѭ�����������ܵı���������_____
(3).����֪�� 2006 �����籭���� 32 ֧�����Ӳμӱ��������ֳ� 8 ��С����ÿ�� 4 �� ������.��һ��ÿ��С����е�ѭ������.���һ�ι� �� Ҫ �� ��_______ ������.
(4).���ֳ� m ��С����ÿ��С���� n ��������һ��ÿ��С����е�ѭ������.��� һ�ι���Ҫ����_____________������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com