
【题目】如图,在![]() 中,
中,![]() ,BD平分
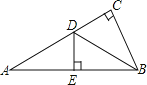
,BD平分![]() ,交AC于点D,DE⊥AB,E为AB的中点,且DE=10cm,则AC=___.
,交AC于点D,DE⊥AB,E为AB的中点,且DE=10cm,则AC=___.
【答案】30cm
【解析】
根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,由等边对等角得出∠ABD=∠A,而BD平分∠ABC,即∠ABD=∠DBC,根据直角三角形两锐角互余得出∠A+∠ABD+∠DBC=90°,求出∠A=30°,根据30°角所对的直角边等于斜边的一半得出AD=2DE=20cm,又角平分线上的点到角的两边的距离相等可得DC=DE=10cm,即可得出结论.
∵DE⊥AB,E为AB的中点,∴DE是斜边AB的垂直平分线,∴AD=BD,∴∠ABD=∠A.
∵∠ABD=∠DBC,∴∠A=∠ABD=∠DBC.
∵在Rt△ABC中,∠C=90°,∴∠A+∠ABD+∠DBC=90°,∴∠A=∠ABD=∠DBC=30°.
∵在Rt△ADE中,∠AED=90°,∠A=30°,DE=10cm,∴AD=2DE=20cm.
∵BD平分∠ABC,∠C=90°,DE⊥AB,∴DC=DE=10cm,∴AC=AD+DC=30cm.
故答案为:30cm.


科目:初中数学 来源: 题型:
【题目】(1)如图1所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.(注意:画得不规范不给分)

从正面看:
从左面看:
(2)如图2,一次数学活动课上,小明用7个棱长为1cm的小立方块积木搭成的几何体,然后他请小亮用尽可能少的同样大小的立方块在旁边再搭一个几何体,使小亮所搭的几何体恰好可以和小明所搭的几何体拼成一个大长方体(即拼大长方体时将其中一个几何体翻转,且假定组成每个几何体的立方块粘合在一起),则:
①小亮至少还需要 个小正方体;
②请画出小明所搭几何体的三视图,并计算①中小亮所搭几何体的表面积.
主视图:
俯视图:
左视图:
查看答案和解析>>
科目:初中数学 来源: 题型:
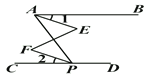
【题目】如图,已知![]() ,
,![]() ,说明
,说明![]() 的理由.
的理由.
解:因为![]() (已知)
(已知)
所以![]() (____________)
(____________)
所以![]() (____________)
(____________)
因为![]() (已知)
(已知)
所以![]() (等式性质)
(等式性质)
即![]()
所以![]() (____________)
(____________)
所以![]() (____________)
(____________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线l1:y=﹣x+n过点A(﹣1,3),双曲线C:y= ![]() (x>0),过点B(1,2),动直线l2:y=kx﹣2k+2(常数k<0)恒过定点F.
(x>0),过点B(1,2),动直线l2:y=kx﹣2k+2(常数k<0)恒过定点F.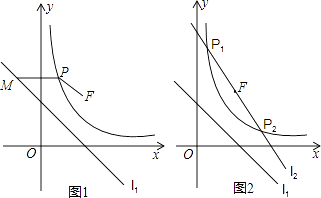
(1)求直线l1 , 双曲线C的解析式,定点F的坐标;
(2)在双曲线C上取一点P(x,y),过P作x轴的平行线交直线l1于M,连接PF.求证:PF=PM.
(3)若动直线l2与双曲线C交于P1 , P2两点,连接OF交直线l1于点E,连接P1E,P2E,求证:EF平分∠P1EP2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区游船码头派车原定于8点整准时到达景区入口接工作人员,由于汽车在路上因故障导致8:10时车还未到达景区入口,于是工作人员步行前往码头.走了一段时间后遇到了前来接他的汽车,他上车后汽车立即掉头继续前进.到达码头时已经比原计划迟到了![]() .已知汽车的速度是工作人员步行速度的6倍,则汽车在路上因故障耽误的时间为____
.已知汽车的速度是工作人员步行速度的6倍,则汽车在路上因故障耽误的时间为____![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 ![]() =2,则
=2,则 ![]() 的值为( )
的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.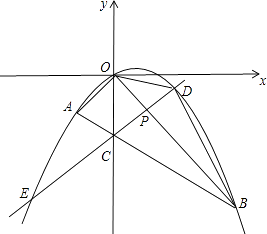
(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com