
����Ŀ�����κ���![]() ��ͼ��y����C������
��ͼ��y����C������![]() ����A��B��������A�ڵ�B�����������A����B�ĺ�������һԪ���η���
����A��B��������A�ڵ�B�����������A����B�ĺ�������һԪ���η���![]() ����������
����������
��1�������A����B�����꼰�ö��κ�������ʽ��

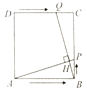
��2����ͼ2������AC��BC����Q���߶�OB��һ����������Q�����O��B�غ���������Q��QD��AC����BC��D����Q��������m��0��������CDQ���S���ʱ����m��ֵ��
��3����ͼ3���߶�MN��ֱ��y=x�ϵĶ��߶�����M�ڵ�N���������MN=![]() ����M��ĺ�����Ϊn������M��x��Ĵ�����x�ύ�ڵ�P������N��x��Ĵ����������߽��ڵ�Q���Ե�P��M��Q��NΪ������ı����ܷ�Ϊƽ���ı��Σ������������n��ֵ������������˵��������
����M��ĺ�����Ϊn������M��x��Ĵ�����x�ύ�ڵ�P������N��x��Ĵ����������߽��ڵ�Q���Ե�P��M��Q��NΪ������ı����ܷ�Ϊƽ���ı��Σ������������n��ֵ������������˵��������
���𰸡���1��A����2��0����B��6��0����![]() ����2��
����2��![]() ����3��n=1��
����3��n=1��![]() ��-1��
��-1��![]() ��
��
�������������������1����һԪ���η���x2-4x-12=0����A��B�������ꣻ��A��B�������������κ���y=ax2+bx+6��������κ�������ʽ��
��2����DQ��AC����BDQ�ס�BCA���������Ʊȱ�ʾ��BDQ����������������������ʽ��ʾ��ACQ�����������S��CDQ=S��ABC-S��BDQ-S��ACQ�����ö��κ�����������������ʱ��m��ֵ��
��3���Ե�P��M��Q��NΪ������ı�����Ϊƽ���ı��Σ���ΪM��N��λ�ò�ȷ��������Ҫ������������ۣ�������������nֵ���ɣ�
�����������1����һԪ���η���x2-4x-12=0�����������ֱ���x=2��6����A����B�ĺ������Ƿ��̵�����������A�ڵ�B����࣬
��A��-2��0����B��6��0������A��B���������������y=ax2+bx+6����
![]() ��
��
���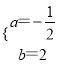 ��
��
��y=-![]() x2+2x+6��
x2+2x+6��
��2�������⣬��AB=8��QB=6-m��AQ=m+2��OC=6����S��ABC=![]() AB��OC=24��
AB��OC=24��
����DQ��AC��
���BDQ�ס�BCA��
��![]() ��
��
��S��BDQ=![]() ��m-6��2��
��m-6��2��
�֡�S��ACQ=![]() AQ��OC=3m+6��
AQ��OC=3m+6��
��S=S��ABC-S��BDQ-S��ACQ=24-![]() ��m-6��2-��3m+6��=-
��m-6��2-��3m+6��=-![]() m2+
m2+![]() m+
m+![]() =-
=-![]() ��m-2��2+6��
��m-2��2+6��
�൱m=2ʱ��S���
��3����MN=![]() ����A��B����ֱ��y=x�ϣ�MN��ֱ��AB�ϣ�MN���߶� AB�ϣ�M�ĺ�����Ϊn��������ҲΪn��
����A��B����ֱ��y=x�ϣ�MN��ֱ��AB�ϣ�MN���߶� AB�ϣ�M�ĺ�����Ϊn��������ҲΪn��
��ͼ3������M��x���ƽ���ߣ�����N��y���ƽ���ߣ������ཻ�ڵ�H��
���MHN�ǵ���ֱ�������Σ�
��MH=NH=1��
���N��������n+1��n+1����
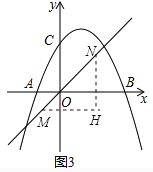
����ͼ4����n��0ʱ��PM=n��
NQ=n+1-[-![]() ��n+1��2+2��n+1��+6]��
��n+1��2+2��n+1��+6]��
���ı���PMQNΪƽ���ı���ʱ��PM=NQ��
��n=n+1-[-![]() ��n+1��2+2��n+1��+6]��
��n+1��2+2��n+1��+6]��
���n=-1+![]() ��
��![]() -1��
-1��
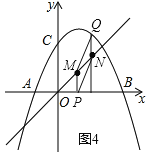
����ͼ5����n��0ʱ��PM=-m��
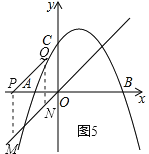
NQ=n+1-[-![]() ��n+1��2+2��n+1��+6]��
��n+1��2+2��n+1��+6]��
���ı���PMQNΪƽ���ı���ʱ��PM=NQ��
��-n=n+1-[-![]() ��n+1��2+2��n+1��+6]��
��n+1��2+2��n+1��+6]��
���n=1-![]() ��n=-1-
��n=-1-![]() ��
��
�ۡ�ֱ��AB��O����ֱ�߾�����һ�������ޣ�
���M�ڵ�3����N�ڵ�2�������ڣ�
���������Ե�P��M��Q��NΪ������ı�����Ϊƽ���ı��Σ�n��ֵ��n=1��![]() ����n=-1��
����n=-1��![]() ��
��


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ�깺��һ���ס������ֿ���ʱ��T���������ֿ�������7800Ԫ�����ֿ�������6400Ԫ�����ֿ��͵ļ��������ֿ��ͼ�����1.5�������ֿ���ÿ���Ľ��۱����ֿ���ÿ���Ľ�����30Ԫ��
��1���ס������ֿ��͵�T�������������ټ���
��2���̵�������60%������ۣ�����һ��ʱ�����ȫ�����꣬�ҿ���ʣ��һ�룬�̵�������ҿ��Ͱ���۵����۽������ۣ��ܿ�ȫ�����꣬������ ����T�����̵깲��������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֿ�Ϊ�˱��ֿ��ڵ�ʪ�Ⱥ��¶ȣ�����ǽ�Ͼ�װ����ͼ��ʾ���Զ�ͨ����ʩ������ʩ���²�ABCD�Ǿ��Σ�����AB=2�ף�BC=1�ף��ϲ���CDG�ǵȱ������Σ��̶���EΪAB���е㣮��EMN���ɵ��Կ�������״�仯������ͨ�細����Ӱ���־���ͨ�磩��MN�ǿ�������ʩ�߿����»�����ʼ�ձ��ֺ�ABƽ�е�������ˣ�
��1����MN��AB֮��ľ���Ϊ0.5��ʱ�����ʱ��EMN�������
��2����MN��AB֮��ľ���Ϊx �ף��Խ���EMN�����S��ƽ���ף���ʾ�ɹ���x�ĺ�����
��3������̽����EMN�����S��ƽ���ף��������ֵ�����У������������ֵ����û�У���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
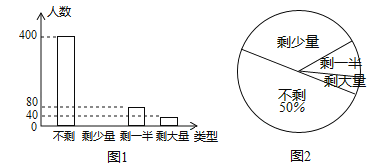
����Ŀ��ij��ҵ���Ὺչ��һ�ܹ���������������������������˲���Ա��һ�ܵĹ�����ʣ�����������������ͳ�ƺ���Ƴ���ͼ 1 ��ͼ 2 ��ʾ�IJ�����ͳ��ͼ ��
��1�� ������Ա��������Ϊ�����ˣ�
��2�� ������ͳ��ͼ����������
��3�� ������ҵ��Ա�� 10000 �ˣ�����Ƹ���ҵij�ܵĹ�����������Ϊ��ʣ��������Ա���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij���ճ�Ϊӭ����һ���������һ��ɱ�Ϊ20Ԫ/���Ĺ���ƷͶ���г����������������������õ�����������
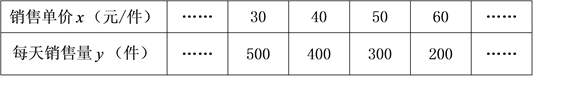
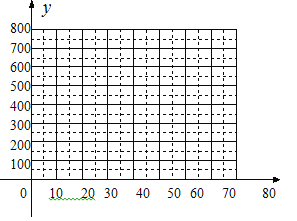
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ����������������ƽ��ֱ������ϵ�������Ӧ�ĵ�������y��x�ĺ�����ϵ�������������ϵʽ��
��2�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ�-�ɱ��ܼ���
��3��������۲��Ź涨���ù���Ʒ���۵��������������45Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪�ı���![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �������Σ�
�������Σ�![]() �������α��ϵ��������㣬��
�������α��ϵ��������㣬��![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���ٶ���
���ٶ���![]() �����˶�����
�����˶�����![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() ������
������![]() �ٶ���
�ٶ���![]() �����˶������
�����˶������![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ��
��
����ͼ1����![]() ��
��![]() ���ϣ�
���ϣ�![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ����ƽ��ʱ����
����ƽ��ʱ����![]() ��ֵ��
��ֵ��
����ͼ2����![]() ��
��![]() ���ϣ�
���ϣ�![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
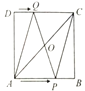
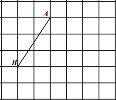
��2����ͼ����С�����εı߳�Ϊ1�������������У���![]() �ڸ���ϣ�
�ڸ���ϣ�
���߶�![]() �ij���_____________��
�ij���_____________��
�������������̶ȵ�ֱ�ߣ���![]() Ϊ������
Ϊ������![]() ��ʹ������ε������
��ʹ������ε������![]() ��
��
Ҫ������ͼ�ۼ�����˵����![]() ��λ������ҵ��ģ�
��λ������ҵ��ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ���Էֱ�����������������
���Էֱ�����������������![]() �����꣮
�����꣮
��1����![]() ��
��![]() ���ϣ�
���ϣ�
��2����![]() �ڹ���
�ڹ���![]() ����
����![]() ��ƽ�е�ֱ���ϣ�
��ƽ�е�ֱ���ϣ�
��3����![]() ����������ľ�����ȣ�
����������ľ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ACB�У���ACB=90�㣬��ABC��ƽ����BE�͡�BAC�����ƽ����AD�ཻ�ڵ�P���ֱ�AC��BC���ӳ�����E��D����P��PF��AD��AC���ӳ����ڵ�H����BC���ӳ����ڵ�F������AF��DH�ڵ�G�������н��ۣ��١�APB=45�㣻��PF=PA����BD��AH=AB����DG=AP+GH��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���Ź�˾�ƻ���A��B��������E����һ��5G�ź�������ʹC��D������ׯ��E�ľ�����ȣ���֪AD��AB�ڵ�A��BC��AB�ڵ�B��AB=80km��AD=50km��BC=30km����5G�ź���EӦ�ý�����A�������ǧ�ĵط���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com