
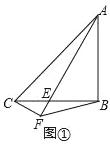
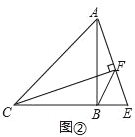
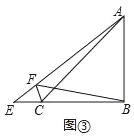
【题目】如图,在△ABC中,∠ABC=90°,AB=BC,点E是直线BC上一点,连接AE,过点C作CF⊥AE于点F,连接BF.如图①,当点E在BC上时,易证AF﹣CF=![]() BF(不需证明),点E在CB的延长线上,如图②:点E在BC的延长线上,如图③,线段AF,CF,BF之间又有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.
BF(不需证明),点E在CB的延长线上,如图②:点E在BC的延长线上,如图③,线段AF,CF,BF之间又有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.
【答案】证明AF=CF+![]() BF.
BF.
如图②中,结论:CF﹣AF=![]() BF.理由见解析;②如图③中,结论:CF+AF=
BF.理由见解析;②如图③中,结论:CF+AF=![]() BF.理由见解析.
BF.理由见解析.
【解析】
如图①中,作BH⊥BF交AF于H.只要证明△BAH![]() △BCF,即可解决问题.
△BCF,即可解决问题.
①如图②中,结论:CF-AF=![]() BF.作BH⊥BF交AF于H.只要证明△BAH
BF.作BH⊥BF交AF于H.只要证明△BAH![]() △BCF,即可解決问題.
△BCF,即可解決问題.
②如图③中,结论:CF+AF=![]() BF,只要证明△BAH
BF,只要证明△BAH![]() △BCF,即可解決问题.
△BCF,即可解決问题.
证明:如图①中,作BH⊥BF交AF于H.
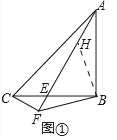
∵∠ABC=∠FBH,
∴∠FBC=∠ABH,
∵∠EFC=∠EBA=90°,
∠CEF=∠AEB,
∴∠ECF=∠EAB,
在△BAH和△BCF中,
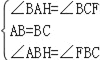 ,
,
∴△BAH≌△BCF,
∴AH=CF,BH=BF,
∵∠FBH=90°,
∴△BFH是等腰直角三角形,
∴FH=![]() BF,
BF,
∵FH=AF﹣AH=AF﹣CF,
∴AF﹣CF=![]() BF,
BF,
∴AF=CF+![]() BF.
BF.
①如图②中,结论:CF﹣AF=![]() BF.
BF.
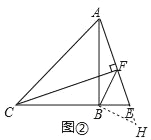
理由:作BH⊥BF交AF于H.
∵∠ABC=∠FBH,
∴∠FBC=∠ABH,
∵∠AFC=∠ABC=90°,
∴∠CEF+∠FCB=90°,∠AEB+∠BAH=90°
∴∠ECF=∠EAB,
在△BAH和△BCF中,
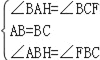 ,
,
∴△BAH≌△BCF,
∴AH=CF,BH=BF,
∵∠FBH=90°,
∴△BFH是等腰直角三角形,
∴FH=![]() BF,
BF,
∵FH=AH﹣AF=CF﹣AF,
∴CF﹣AF=![]() BF.
BF.
②如图③中,结论:CF+AF=![]() BF.
BF.
理由:作BH⊥BF交AF于H.
∵∠ABC=∠FBH,
∴∠FBC=∠ABH,
∵∠AFC=∠ABC=90°,
∴∠BCF+∠BAF=180°,∵∠BAF+∠BAH=180°
∴∠BCF=∠BAH,
在△BAH和△BCF中,
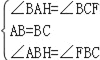 ,
,
∴△BAH≌△BCF,
∴AH=CF,BH=BF,
∵∠FBH=90°,
∴△BFH是等腰直角三角形,
∴FH=![]() BF,
BF,
∵FH=AH+AF=CF+AF,
∴CF+AF=![]() BF.
BF.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E点.

(1)当∠BDA=115°时,∠BAD=___°,∠DEC=___°;
(2)当DC等于多少时,△ABD与△DCE全等?请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,

(1)求证:△ABQ ≌ △CAP;
(2)∠CMQ的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)连接PQ,当点P,Q运动多少秒时,△PBQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com