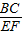在等腰△ABC与等腰△DEF中,有AB=AC>BC,DE=DF>EF,且AB≠DE.请判断下面两个命题是否正确.若正确,请证明;若不正确,请举一个反例说明.
命题1:如果∠A+∠B=∠D+∠E,那么等腰△ABC与等腰△DEF相似;
命题2:如果AB+BC=DE+EF,那么等腰△ABC与等腰△DEF相似.
【答案】
分析:(1)根据三角形内角和性质可以求得∠C=∠F,即可求证∠B=∠C、∠E=∠F,即可判定等腰△ABC与等腰△DEF相似;
(2)举出一个反例,并且证明其不相似即可解题.
解答:(1)正确.
证明:∵∠A+∠B+∠C=180°=∠D+∠E+∠F=180°,
又∵∠A+∠B=∠D+∠E,
∴∠C=∠F.
∵在等腰△ABC与等腰△DEF中,有∠B=∠C,∠E=∠F,
∴等腰△ABC与等腰△DEF相似;
(2)不正确
反例:当AB=AC=5>BC=3,DE=DF=7>EF=1时,
等腰△ABC与等腰△DEF不相似.
说明:∵当AB=AC=5>BC=3,DE=DF=7>EF=1时,
尽管有AB+BC=DE+EF,
但是
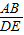
=
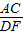
≠
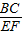
∴等腰△ABC与等腰△DEF不相似,即命题2不正确.
点评:本题考查了等腰三角形底角相等的性质,相似三角形的判定,本题中证明∠B=∠C、∠E=∠F是解题的关键.

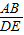 =
=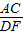 ≠
≠