
科目:初中数学 来源: 题型:解答题
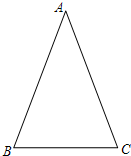 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化. .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C. D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.查看答案和解析>>
科目:初中数学 来源:2012年安徽省芜湖市保沙中学参加县一中自主招生考试数学模拟试卷(解析版) 题型:解答题
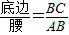 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C.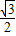 D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.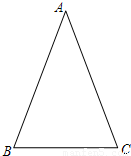
查看答案和解析>>
科目:初中数学 来源:2012年易学教育中考数学模拟试卷(13)(解析版) 题型:解答题
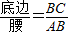 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C.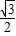 D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.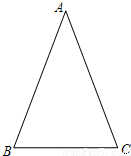
查看答案和解析>>
科目:初中数学 来源:2011年广东省初中毕业生学业仿真考试数学试卷(解析版) 题型:解答题
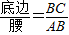 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C.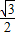 D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.
查看答案和解析>>
科目:初中数学 来源:2011年安徽省巢湖市初中毕业班十校联考数学试卷(解析版) 题型:解答题
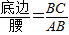 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C.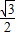 D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.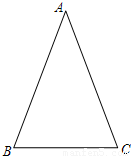
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com