
【题目】计算下列各题
(1)![]() ﹣3tan30°+(4﹣π)0﹣(
﹣3tan30°+(4﹣π)0﹣( ![]() )﹣1
)﹣1
(2)先化简,再求值:( ![]() ﹣x+1)÷
﹣x+1)÷ ![]() ,其中x=
,其中x= ![]() ﹣2.
﹣2.
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里,有5个除颜色外,其他都相同的小球.其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则有一次取到绿球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
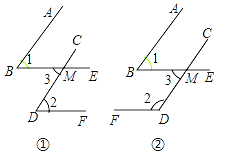
【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).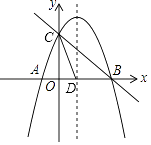
(1)求抛物线的解析式
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,请直接写出P点的坐标;如果不存在,请说明理由.
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?请求出△CBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
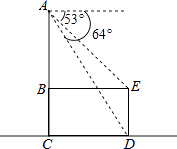
【题目】如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?
(参考数据:tan53°≈ ![]() ,sin53°≈
,sin53°≈ ![]() ,tan64°≈2,sin64°≈
,tan64°≈2,sin64°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
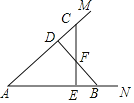
【题目】如图,C,D和E,B分别是∠MAN的边AM和AN上的两点,且AC=AB,AD=AE,CE和BD相交于F点,给出下列结论:①△ABD≌△ACE;②△BFE≌△CFD;③F在∠MAN的平分线上.其中正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
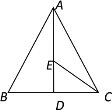
【题目】如图所示,在等边三角形ABC中,BC边上的高AD=10,E是AD上一点,现有一动点P沿着折线A-E-C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A到C的运动过程中至少需_______秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
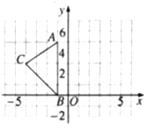
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);
⑵直接写出A’,B’,C’三点的坐标:A’ ( ),B’( ),C’( );
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com