
【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A、B、C三点的坐标及抛物线的对称轴;
(2)若已知x轴上一点N( ![]() ,0),则在抛物线的对称轴上是否存在一点Q,使得△CNQ是直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
,0),则在抛物线的对称轴上是否存在一点Q,使得△CNQ是直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:由y=﹣x2+2x+3得到:y=﹣(x+1)(x﹣3),或y=﹣(x﹣1)2+4,
则A(﹣1,0),B(3,0),对称轴是x=1.
令x=0,则y=3,
所以C(0,3),
综上所述,A(﹣1,0),B(3,0),C(0,3),对称轴是x=1
(2)解:假设存在满足条件的点Q.
设Q(1,m).
又(0,3),
∴CN2=32+( ![]() )2=
)2= ![]() ,CQ2=12+(3﹣m)2=m2﹣6m+10.NQ2=(
,CQ2=12+(3﹣m)2=m2﹣6m+10.NQ2=( ![]() ﹣1)2+m2=
﹣1)2+m2= ![]() +m2.
+m2.
①当点C是直角顶点时,则CN2+CQ2=NQ2,即 ![]() +m2﹣6m+10=
+m2﹣6m+10= ![]() +m2.
+m2.
解得m= ![]() ,
,
此时点Q的坐标是(1, ![]() );
);
②当点N为直角顶点时,CN2+NQ2=CQ2,即 ![]() +
+ ![]() +m2=m2﹣6m+10
+m2=m2﹣6m+10
解得m=﹣ ![]() ,
,
此时点Q的坐标是(1,﹣ ![]() );
);
③当点Q为直角顶点时,CQ2+NQ2=CN2,即 ![]() =
= ![]() +m2+m2﹣6m+10
+m2+m2﹣6m+10
解得m= ![]() 或m=
或m= ![]() ,
,
此时点Q的坐标是(1, ![]() )或(1,
)或(1, ![]() ).
).
综上所述,满足条件的点Q的坐标为:(1, ![]() )或(1,﹣
)或(1,﹣ ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )
)
【解析】(1)分别令y=0,x=0,可求出抛物线与x轴、y轴交点坐标;利用对称轴公式x=-![]() ,求出对称轴;(2)“是否存在”问题的基本解决方案法为:假设存在满足条件的点Q,△CNQ是直角三角形可分为三类:①当点C是直角顶点时②当点N为直角顶点时③当点Q为直角顶点时,再利用勾股定理列出方程,得出答案.
,求出对称轴;(2)“是否存在”问题的基本解决方案法为:假设存在满足条件的点Q,△CNQ是直角三角形可分为三类:①当点C是直角顶点时②当点N为直角顶点时③当点Q为直角顶点时,再利用勾股定理列出方程,得出答案.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点O为对角线AC的中点,过点o作射线OG、ON分别交AB,BC于点E,F,且∠EOF=90°,BO、EF交于点P.则下列结论中:
⑴图形中全等的三角形只有两对;
⑵正方形ABCD的面积等于四边形OEBF面积的4倍;
⑶BE+BF= ![]() OA;
OA;
⑷AE2+CF2=2OPOB.
正确的结论有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知⊙A经过点E,B,C,O,且C(0,6)、E(﹣8,0)、O(0,0),则cos∠OBC的值为( )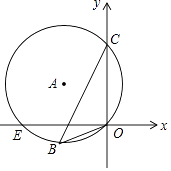
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“湘一四边形”.
(1)已知:如图1,四边形![]() 是“湘一四边形”,
是“湘一四边形”,![]() ,
,![]() ,
,![]() .则
.则![]() ,
, ![]() ,若
,若![]() ,
,![]() ,则
,则![]() (直接写答案)
(直接写答案)
(2)已知:在“湘一四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .求对角线
.求对角线![]() 的长(请画图求解),
的长(请画图求解),
(3)如图(2)所示,在四边形![]() 中,若
中,若![]() ,当
,当![]() 时,此时四边形
时,此时四边形![]() 是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
是否是“湘一四边形”,若是,请说明理由:若不是,请进一步判断它的形状,并给出证明.
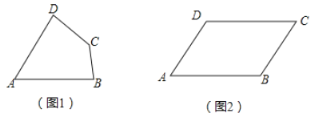
查看答案和解析>>
科目:初中数学 来源: 题型:
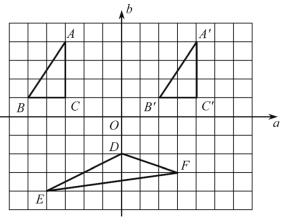
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的变换得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请求出三角形DEF的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
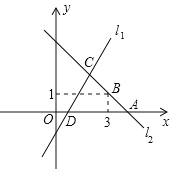
【题目】如图,直线l1的函数解析式为y=2x–2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B(3,1),如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)利用函数图象写出关于x、y的二元一次方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市荸荠喜获丰收,某生产基地收获荸荠40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 批发 零售 加工销售
利润(百元/吨) 12 22 30
设按计划全部售出后的总利润为y百元,其中批发量为x吨,且加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com