
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃垂直于墙的一边长为x米.
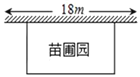
(1)若苗圃的面积为72平方米,求x的值;
(2)这个苗圃的面积能否是120平方米?请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).
(1)小红摸出标有数3的小球的概率是多少?.
(2)请你用列表法或画树状图法表示出由x,y确定的点P(x,y)所有可能的结果.
(3)求点P(x,y)在函数y=﹣x+5图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+3)x+m+1=0.
(1)求证:不论m为何值,方程都有两个不相等的实数根;
(2)若方程一根为4,以此时方程两根为等腰三角形两边长,求此三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
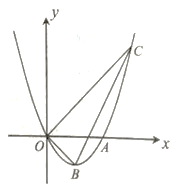
【题目】如图,抛物线![]() 过原点,且与
过原点,且与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)已知![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)在第一象限的抛物线上是否存在一点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似,若存在,求出满足条件的点
相似,若存在,求出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.

(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6,点E边BC上,连接AE,将△ABE沿着AE翻折到△AEF,连接CF、DF,若△CDF为等腰三角形,则△CDF的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解10—60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:


(1)请直接写出![]() 、
、![]() 的值及扇形统计图中第3组所对应的圆心角的度数;
的值及扇形统计图中第3组所对应的圆心角的度数;
(2)请补全上面的频数分布直方图;
(3)假设该市现有10—60岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=![]() x2+
x2+![]() x﹣4
x﹣4![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,作直线AC.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,作直线AC.
(1)如图1,点P是直线AC下方抛物线上的一点,连结PA,PC.过点P作PD⊥AC于点D,交y轴于点M,E是射线PD上的一点,Q是x轴上的一点,F是y轴上的一点,过F作该抛物线对称轴的垂线段,垂足为点G,连结EF,GQ.当△PAC面积最大时,求点P的坐标,并求EF+GQ+![]() (FG+QA)的最小值;
(FG+QA)的最小值;
(2)如图2,在(1)的条件下,将△CDM绕点D旋转得到△C'DM',在旋转过程中,当点C'或点M′落在y轴上(不与点M、C重合)时,将△C'DM'沿射线PD平移得到△C″D'M″,在平移过程中,平面内是否存在点N,使得四边形OM″NC″是菱形?若存在,请直接写出所有符合条件的点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com