
 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=8,∠BAC+∠EAD=180°,则弦BC的弦心距等于4.
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=8,∠BAC+∠EAD=180°,则弦BC的弦心距等于4. 分析 作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,再证明△ADE≌△ABF,得到DE=BF=8,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=$\frac{1}{2}$BF=4.
解答 解:如图,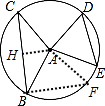
作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,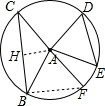
∴$\widehat{DE}$=$\widehat{BF}$,
∴DE=BF=8,
∵AH⊥BC,
∴CH=BH,
而CA=AF,
∴AH为△CBF的中位线,
∴AH=$\frac{1}{2}$BF=4.
故答案为:4.
点评 本题考查了垂径定理和三角形中位线性质,以及圆周角定理,关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


科目:初中数学 来源:2017届江苏省徐州市九年级下学期第一次(3月)月考数学试卷(解析版) 题型:单选题
如图,一个正六边形转盘被分成6个全等的正三角形.任意旋转这个转盘1次,当转盘停止转动时,指针指向阴影区域的概率是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
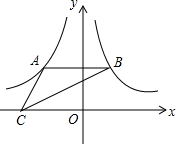 如图,AB平行于x轴,点A在反比例函数$y=-\frac{4}{x}$的图象上,点B在反比例函数$y=\frac{3}{x}$的图象上,点C在x轴上,则△ABC的面积为( )
如图,AB平行于x轴,点A在反比例函数$y=-\frac{4}{x}$的图象上,点B在反比例函数$y=\frac{3}{x}$的图象上,点C在x轴上,则△ABC的面积为( )| A. | $\frac{7}{3}$ | B. | 7 | C. | $\frac{7}{4}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com