
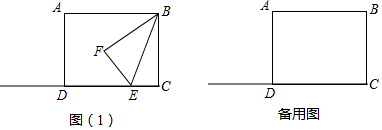
分析 (1)如图1中,MN是线段AD的中垂线,作FH⊥CD于H.设CE=EF=x,在Rt△EFH中,根据EF2=FH2+HE2,构建方程即可解决问题.
(2)如图2中,MN是线段AB的中垂线,设EF=CE=x.在Rt△EFN中,根据EF2=FN2+NE2,构建方程即可解决问题.
(3)欲求CG的最大值,只要求出DG的最小值即可,由DG=AD•tan∠GAD,推出∠GAD最小时,DG的值最小,由BF=BC,BF是定值,推出当BF⊥AG时,∠BAF的值最大,即∠DAG的值最小,当BF⊥AG时,易知点E与点G共点,设CG=GF=x,在Rt△ADE中,根据AD2+DG2=AG2,构建方程即可解决问题.
解答 解:(1)如图1中,MN是线段AD的中垂线,作FH⊥CD于H.
在Rt△BFM中,∵BF=BC=3,BM=$\frac{3}{2}$,
∴FM=CH=$\sqrt{B{F}^{2}-B{M}^{2}}$=$\frac{3\sqrt{3}}{2}$,设CE=EF=x,
在Rt△EFH中,∵EF2=FH2+HE2,
∴x2=($\frac{3}{2}$)2+($\frac{3\sqrt{3}}{2}$-x)2,
∴x=$\sqrt{3}$,
∴CE=$\sqrt{3}$.
(2)如图2中,MN是线段AB的中垂线,设EF=CE=x.
在Rt△BFM中,∵∠BMF=90°,BM=2,BF=BC=3,
∴MF=$\sqrt{B{F}^{2}-B{M}^{2}}$=$\sqrt{5}$,
∵MN=BC=3,
∴FN=3-$\sqrt{5}$,EN=2-x,
在Rt△EFN中,∵EF2=FN2+NE2,
∴x2=(3-$\sqrt{5}$)2+(2-x)2,
∴x=$\frac{9-3\sqrt{5}}{2}$.
(3)如图3中,
欲求CG的最大值,只要求出DG的最小值即可,
∵DG=AD•tan∠GAD,
∴∠GAD最小时,DG的值最小,
∵BF=BC,BF是定值,
∴当BF⊥AG时,∠BAF的值最大,即∠DAG的值最小,
当BF⊥AG时,易知点E与点G共点,
设CG=GF=x,
在Rt△ABF中,∵∠AFB=90°,AB=4,BF=BC=3,
∴AF=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
在Rt△ADE中,∵AD2+DG2=AG2,
∴32+(4-x)2=($\sqrt{7}$+x)2,
∴x=4-$\sqrt{7}$.
∴CG的最大值为4-$\sqrt{7}$,
故答案为4-$\sqrt{7}$.
点评 本题考查四边形综合题、翻折变换、矩形的性质、勾股定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用构建方程的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
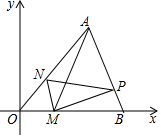 如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(6,6),O(0,0),B(8,0).点M是OB边上异于O,B的一动点,MN∥AB交OA于点N,点P是AB边上任意点,连接AM,PM,PN,BN.设点M的坐标是(t,0),△PMN的面积为S.
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(6,6),O(0,0),B(8,0).点M是OB边上异于O,B的一动点,MN∥AB交OA于点N,点P是AB边上任意点,连接AM,PM,PN,BN.设点M的坐标是(t,0),△PMN的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组号 | 分组 | 频数 |
| 一 | 6≤m<7 | 2 |
| 二 | 7≤m<8 | 7 |
| 三 | 8≤m<9 | a |
| 四 | 9≤m≤10 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
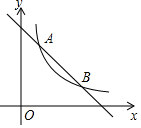 如图,一次函数y=-x+3的图象与反比例y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+3的图象与反比例y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com