
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
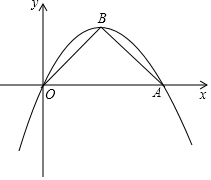 如图,在平面直角坐标系xOy,已知二次函数y=-$\frac{1}{2}$x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
如图,在平面直角坐标系xOy,已知二次函数y=-$\frac{1}{2}$x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
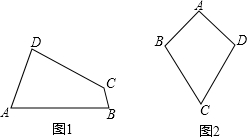
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
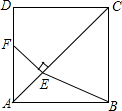 如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 植树数量(棵) | 4 | 5 | 6 | 8 | 10 |
| 人数 | 30 | 26 | 25 | 15 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
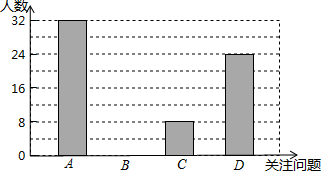 6月5日是世界环境日,2017年世界环境日中国的主题是“绿水青山就是金山银山”,小明积极学习与宣传,并从四个方面(A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖)对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),并绘制了如下不完整的统计图表:
6月5日是世界环境日,2017年世界环境日中国的主题是“绿水青山就是金山银山”,小明积极学习与宣传,并从四个方面(A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖)对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),并绘制了如下不完整的统计图表:| 关注的问题 | 频数 | 频率 |
| A | 32 | m |
| B | a | 0.2 |
| C | 8 | 0.1 |
| D | 24 | n |
| 合计 | b | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com