
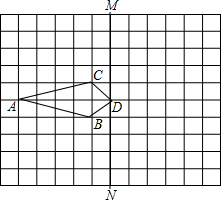
 ��ͼ���ı���ABDC���ĸ����㶼�������������е�С�����ζ����ϣ�ÿ��С�����εı߳�Ϊ1��
��ͼ���ı���ABDC���ĸ����㶼�������������е�С�����ζ����ϣ�ÿ��С�����εı߳�Ϊ1������ ��1���ֱ�������A��B��D��C����ƽ��1����λ��������ƽ��4����λ�õ��Ķ�Ӧ�㣬˳�����Ӽ��ɵã�
��2���ֱ�������A��B��C����ֱ��MN���ۺ�õ��Ķ�Ӧ�㣬˳�����Ӽ��ɵã��ٸ��ݹ��ɶ����ɵ�D1A2�ij��ȣ�
��� �⣺��1����ͼ���ı���A1B1D1C1��Ϊ����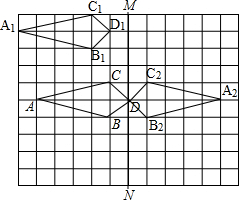
��2����ͼ���ı���A2B2DC2��Ϊ����D1A2=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$��
���� ���⿼�������ͼ-ƽ�Ʊ任����ԳƱ任����֪ͼ��ƽ�Ʋ����Ե����ʺ���Գ������ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
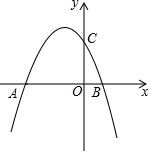 ��ͼ����֪������y=-$\frac{1}{3}$x2+bx+6��x�ύ�ڵ�A��-6��0���͵�B����y�ύ�ڵ�C��
��ͼ����֪������y=-$\frac{1}{3}$x2+bx+6��x�ύ�ڵ�A��-6��0���͵�B����y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
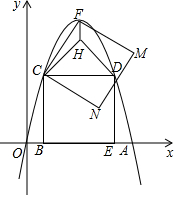 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2-6ax��a��0����x�������ύ�ڵ�A������BCDE�Ķ���B��E����x���ϣ�C��D�����������ϣ��ҵ�B������Ϊ��1��0���������ߵĶ���ΪF����CFΪ����������CFMN����CDΪ�ױ�����������ֱ��������CDH������FH��
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2-6ax��a��0����x�������ύ�ڵ�A������BCDE�Ķ���B��E����x���ϣ�C��D�����������ϣ��ҵ�B������Ϊ��1��0���������ߵĶ���ΪF����CFΪ����������CFMN����CDΪ�ױ�����������ֱ��������CDH������FH���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ƽ���ı���ABCD�У�����D��DE��AB�ڵ�E����F��CD�ϣ�CF=AE������BF��AF��
ƽ���ı���ABCD�У�����D��DE��AB�ڵ�E����F��CD�ϣ�CF=AE������BF��AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
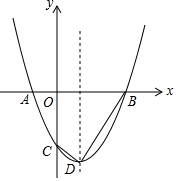 ��ͼ��O������ԭ�㣬����A��-1��0����������y=x2-bx-3��x�����һ������ΪB����y�ύ�ڵ�C���䶥��ΪD��
��ͼ��O������ԭ�㣬����A��-1��0����������y=x2-bx-3��x�����һ������ΪB����y�ύ�ڵ�C���䶥��ΪD���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com