练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．下列说法中不正确的是（　　）
    A．在平面内，两条互相垂直、原点重合的数轴的垂足是原点
    B．平面直角坐标系所在平面叫坐标平面
    C．坐标平面上的点与有序数对是一一对应的
    D．凡是两条互相垂直的直线都能组成平面直角坐标系

    分析 根据平面直角坐标系，点与平面直角坐标系的关系，可得答案．

    解答 解：在平面内，两条互相垂直、原点重合的数轴的垂足是原点，
    平面直角坐标系所在平面叫坐标平面；
    坐标平面上的点与有序数对是一一对应的
    在平面内，两条互相垂直、原点重合的数轴组成平面直角坐标系，
    故D不符合题意；
    故选：D．

    点评 本题考查了平面直角坐标系，利用平面直角坐标系的意义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．某校九年级数学兴趣小组的活动课题是“测量物体高度”．小组成员小明与小红分别采用不同的方案测量同一个底面为圆形的古塔高度，以下是他们研究报告的部分记录内容：
    课题：测量古塔的高度
    小明的研究报告小红的研究报告
    图示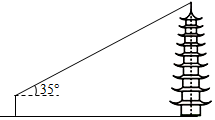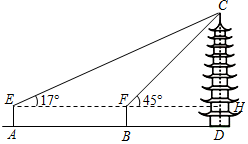
    测量方案与测量数据　  用距离地面高度为1.6m的测角器测出古塔顶端的仰角为35°，再用皮尺测得测角器所在位置与古塔底部边缘的最短距离为30m．在点A用距离地面高度为1.6m的测角器测出古塔顶端的仰角为17°，然后沿AD方向走58.8m到达点B，测出古塔顶端的仰角为45°．
    参考数据sin35°≈0.57，cos35°≈0.82，tan35°≈0.70sin17°≈0.29，cos17°≈0.96，tan17°≈0.30，$\sqrt{2}$≈1.41
    计算古塔高度
    （结果精确到0.1m）    		30×tan35°+1.6≈22.6（m）
    （1）写出小红研究报告中“计算古塔高度”的解答过程；
    （2）数学老师说小红的结果较准确，而小明的结果与古塔的实际高度偏差较大．针对小明的测量方案分析测量发生偏差的原因；
    （3）利用小明与小红的测量数据，估算该古塔底面圆直径的长度为8.4m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知y=y1+y2，而y1与x+1成正比例，y2与x2成正比例，并且x=1时，y=2；x=0时，y=2，求y与x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．若$\sqrt{x}$+$\sqrt{\frac{1}{x}}$=$\sqrt{6}$，x≥1，则$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=（　　）
    A．±2B．-$\sqrt{2}$C．$\sqrt{2}$D．$±\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

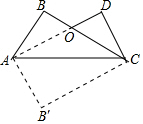    9．把长方形AB′CD沿对角线AC折叠，得到如图所示的图形，已知∠BAO=30°，
    （1）求∠AOC和∠BAC的度数；
    （2）若AD=3$\sqrt{3}$，OD=$\sqrt{3}$，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．一组数据2，x，4，3，3的平均数是3，则这组数据的方差是0.4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．在平面直角坐标系中，点O是坐标原点，点A的坐标是（-a，a），点B的坐标是（c，b），满足$\left\{\begin{array}{l}{3a-b+2c=8}\\{a-2b-c=-4}\end{array}\right.$．
    （1）若x=2是3x-a＜0的一个解，试判断点A在第几象限，并说明理由；
    （2）若△AOB的面积是4，求点B的坐标；
    （3）若两个动点E（e，2e+1）、F（ f，-2f+3），请你探索是否存在以两个动点E、F为端点的线段EF∥AB，且EF=AB？若存在，求出E、F两点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，在△ABC中，AD⊥BC于点D，AD=BC，以AB为底边作等腰Rt△ABE，连接ED，EC，延长CE交AD于点F，下列结论：①△ADE≌△BCE；②BD+DF=AD；③CE⊥DE；④S△BDE=S△ACE，其中正确的有①②③④（填写正确的番号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．当a$≠-\frac{3}{2}$时，分式$\frac{a-1}{2a+3}$有意义．若分式$\frac{|x|-3}{x-3}$的值为0，则x=-3．

    查看答案和解析>>

    同步练习册答案