
| 所购苹果数量 | 不超过30千克 | 30千克以上但不超过50千克 | 50千克以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
分析 (1)根据售价分别计算甲班、乙班的付费数额,然后作出差即可;
(2)设第一次购买苹果x千克,第二次购买苹果(60-x)千克,应分情况进行讨论:①第二次30千克以上,但不超过50千克;②第二次是50千克以上,分别列方程求解可得.
解答 解:(1)甲班的费用:28×3+30×3+2×2.5=179(元),
乙班的费用:30×3+20×2.5+10×2=160(元),
则179-160=19(元)
答:乙班比甲班少付19元.
(2)设第一次购买苹果x千克,则第二次购买苹果(60-x)千克,
依题意知,0≤x<30,
①当30<60-x≤50,即10≤x<30时,3x+2.5(60-x)=163,
解得:x=26;
②当60-x>50,即0≤x<10,3x+2(60-x)=163,
解得:x=43>10,舍去;
答:甲第一次购买苹果26千克,第二次购买苹果34千克.
点评 本题主要考查一元一次方程的应用,解题关键是弄清题意,找到合适的等量关系:甲班分两次共购买苹果60千克(第二次多于第一次),共付费163元.注意合理分析各种情况得出结论.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
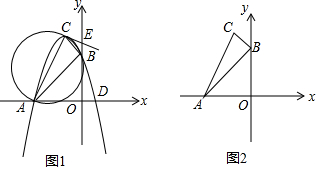
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )
如图,坐标系中抛物线是函数y=ax2+bx+c的图象,则下列式子能成立的是( )| A. | abc>0 | B. | a+b+c<0 | C. | b<a+c | D. | 4a+2b+c>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
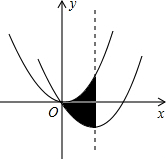 如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.
如图,在平面直角坐标系中,将抛物线y=$\frac{1}{2}$x2经过平移得到抛物线y=$\frac{1}{2}$x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 实验与探究:三角点阵前n行的点数计算.
实验与探究:三角点阵前n行的点数计算.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com