
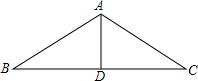
 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10m,中柱AD(D为BC中点)的长是3.6m,则∠BAC=108°(用科学计算器计算,结果精确到1°).
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10m,中柱AD(D为BC中点)的长是3.6m,则∠BAC=108°(用科学计算器计算,结果精确到1°). 科目:初中数学 来源: 题型:解答题
 已知点A(-1,0),点B(4,0),点C在y轴的正半轴上,且∠ACB=90°.抛物线y=ax2+bx+c经过A、B、C三点,且顶点为M.
已知点A(-1,0),点B(4,0),点C在y轴的正半轴上,且∠ACB=90°.抛物线y=ax2+bx+c经过A、B、C三点,且顶点为M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 嘉淇同学家的饮水机中原有水的温度为20℃,其工作过程如图所示,在一个由20℃加热到100℃再降温到20℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分钟),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.
嘉淇同学家的饮水机中原有水的温度为20℃,其工作过程如图所示,在一个由20℃加热到100℃再降温到20℃的过程中,水温记作y(℃),从开始加热起时间变化了x(分钟),加热过程中,y与x满足一次函数关系,水温下降过程中,y与x成反比例,当x=20时,y=40.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | 1-$\frac{3\sqrt{2}π}{16}$ | B. | $\sqrt{2}-\frac{3π}{8}$ | C. | 1-$\frac{3π}{8}$ | D. | $\frac{3π}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>1 | B. | m≥1 | C. | m≥-1且m≠1 | D. | m>-1且m≠1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com