
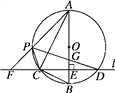
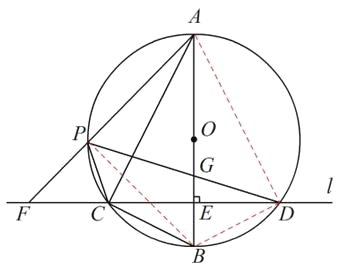
【题目】如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是![]() 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:△PAC∽△PDF;
(2)若AB=5,![]() ,求PD的长;
,求PD的长;
(3)在点P运动过程中,设![]() =x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)
=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)应用圆周角定理证明∠APD=∠FPC,得到∠APC=∠FPD,又由∠PAC=∠PDC,即可证明结论.
(2)由AC=2BC,设![]() ,应用勾股定理即可求得BC,AC的长,则由AC=2BC得
,应用勾股定理即可求得BC,AC的长,则由AC=2BC得![]() ,由△ACE∽△ABC可求得AE,CE的长,由
,由△ACE∽△ABC可求得AE,CE的长,由![]() 可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得
可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得![]() ,即可求得PD的长.
,即可求得PD的长.
(3)连接BP,BD,AD,根据圆的对称性,可得![]() ,由角的转换可得
,由角的转换可得![]() ,由△AGP∽△DGB可得
,由△AGP∽△DGB可得![]() ,由△AGD∽△PGB可得
,由△AGD∽△PGB可得![]() ,两式相乘可得结果.
,两式相乘可得结果.
试题解析:(1)由APCB内接于圆O,得∠FPC=∠B,
又∵∠B=∠ACE=90°-∠BCE,∠ACE=∠APD,∴∠APD=∠FPC.
∴∠APD+∠DPC=∠FPC+∠DPC,即∠APC=∠FPD.
又∵∠PAC=∠PDC,∴△PAC∽△PDF.
(2)连接BP,设![]() ,∵∠ACB=90°,AB=5,∴
,∵∠ACB=90°,AB=5,∴![]() .∴
.∴![]() .
.
∵△ACE∽△ABC,∴![]() ,即
,即![]() . ∴
. ∴![]() .
.
∵AB⊥CD,∴![]() .
.
如图,连接BP,
∵![]() ,∴△APB是等腰直角三角形. ∴∠PAB=45°,
,∴△APB是等腰直角三角形. ∴∠PAB=45°,![]() .
.
∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.
由(1)△PAC∽△PDF得![]() ,即
,即![]() .
.
∴PD的长为![]() .
.
(3)如图,连接BP,BD,AD,
∵AC=2BC,∴根据圆的对称性,得AD=2DB,即![]() .
.
∵AB⊥CD,BP⊥AE,∴∠ABP=∠AFD.
∵![]() ,∴
,∴![]() .
.
∵△AGP∽△DGB,∴![]() .
.
∵△AGD∽△PGB,∴![]() .
.
∴![]() ,即
,即![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
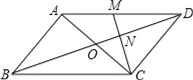
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
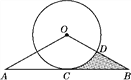
【题目】如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )

A.9 B.10 C.3![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D.已知OA=OB=6 cm,AB=6![]() cm.
cm.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式![]() .
.
(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,![]() ),使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
),使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com