

|
|
|


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
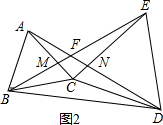
 如图,AB=BC,∠ABC=90°,∠ABE=∠AEB,AD⊥BE,AE=EF,∠AEF=90°,CF交BE延长线于点M,探究FM与CM的数量关系.
如图,AB=BC,∠ABC=90°,∠ABE=∠AEB,AD⊥BE,AE=EF,∠AEF=90°,CF交BE延长线于点M,探究FM与CM的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某农场要利用一面墙(墙长为50米)建蔬菜实验田,用120米的围栏围成总面积为800平方米的三个大小、形状完全相同的矩形实验田,种植三种不同的蔬菜,求实验田的边长AB、BC各为多少米?
如图,某农场要利用一面墙(墙长为50米)建蔬菜实验田,用120米的围栏围成总面积为800平方米的三个大小、形状完全相同的矩形实验田,种植三种不同的蔬菜,求实验田的边长AB、BC各为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:
| A、42.1×106米 |
| B、421×106米 |
| C、0.421×108米 |
| D、4.21×107米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| m |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
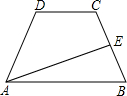 如图,已知E是等腰梯形ABCD的腰BC的中点,AE把梯形分成四边形AECD和△AEB,且四边形AECD的周长比△AEB周长要多4cm,若AB=12cm,CD=2cm,求梯形的腰AD长.
如图,已知E是等腰梯形ABCD的腰BC的中点,AE把梯形分成四边形AECD和△AEB,且四边形AECD的周长比△AEB周长要多4cm,若AB=12cm,CD=2cm,求梯形的腰AD长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com