练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】今年下半年以来，猪肉价格不断上涨，主要是由非洲猪瘟疫情导致．非洲猪瘟疫情发病急，蔓延速度快．某养猪场第一天发现3头生猪发病，两天后发现共有192头生猪发病．

    （1）求每头发病生猪平均每天传染多少头生猪？

    （2）若疫情得不到有效控制，按照这样的传染速度，3天后生猪发病头数会超过1500头吗？

    【答案】（1）7头；（2）会超过1500头

    【解析】

    （1）设每头发病生猪平均每天传染x头生猪，根据“第一天发现3头生猪发病，两天后发现共有192头生猪发病”，即可得出关于x的一元二次方程，解之取其正值即可得出结论；
    （2）根据3天后生猪发病头数=2天后生猪发病头数×（1+7），即可求出3天后生猪发病头数，再将其与1500进行比较即可得出结论．

    解：（1）设每头发病生猪平均每天传染头生猪，

    依题意，得，

    解得：， （不合题意，舍去）．

    答：每头发病生猪平均每天传染7头生猪．

    （2）（头，．

    答：若疫情得不到有效控制，3天后生猪发病头数会超过1500头．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与直线相交于，两点，且抛物线经过点

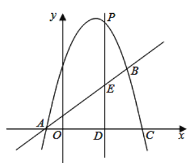
    （1）求抛物线的解析式．

    （2）点是抛物线上的一个动点（不与点点重合），过点作直线轴于点，交直线于点．当时，求点坐标；

    （3）如图所示，设抛物线与轴交于点，在抛物线的第一象限内，是否存在一点，使得四边形的面积最大？若存在，请求出点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】廊桥是我国古老的文化遗产．如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为，为保护廊桥的安全，在该抛物线上距水面高为8米的点、处要安装两盏警示灯，则这两盏灯的水平距离是____米．

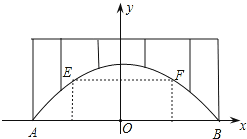
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图, 在等边△ABC中, D, E, F分别为边AB, BC, CA上的点, 且满足∠DEF=60°．

    （1）求证：；

    （2）若DE⊥BC且DE=EF, 求的值．

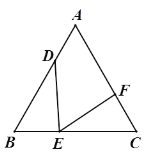
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙M的半径为4，圆心M的坐标为（6，8），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班“数学兴趣小组”对函数的图像和性质进行了探究，探究过程如下，请补充完整．

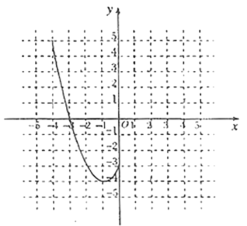
    （1）自变量的取值范围是全体实数，与的几组对应值列表如下：

    其中，________________．

    （2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图像的一部分，请画出该图像的另一部分；

    （3）观察函数图像，写出两条函数的性质；

    （4）进一步探究函数图像发现：

    ①方程有______个实数根；

    ②函数图像与直线有_______个交点，所以对应方程有_____个实数根；

    ③关于的方程有个实数根，的取值范围是___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝ax2+bx+c（a＞0）的顶点为M，直线y＝m与抛物线交于点A，B，若△AMB为等腰直角三角形，我们把抛物线上A，B两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形，线段AB称为碟宽，顶点M 称为碟顶．

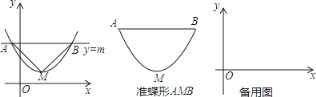
    （1）由定义知，取AB中点N，连结MN，MN与AB的关系是_____．

    （2）抛物线y＝对应的准蝶形必经过B（m，m），则m＝_____，对应的碟宽AB是_____．

    （3）抛物线y＝ax2﹣4a﹣（a＞0）对应的碟宽在x 轴上，且AB＝6．

    ①求抛物线的解析式；

    ②在此抛物线的对称轴上是否有这样的点P（xp，yp），使得∠APB为锐角，若有，请求出yp的取值范围．若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂生产一种火爆的网红电子产品，每件产品成本 16 元，工厂将该产品进行网络批发，批发单价 y（元）与一次性批发量 x（件）（x为正整数）之间满 足如图所示的函数关系．

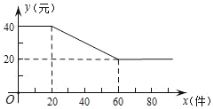
    （1）直接写出 y与 x之间所满足的函数关系式，并写出自变量 x的取值范围；

    （2）若一次性批发量不低于 20 且不超过 60 件时，求获得的利润 w 与 x 的函数 关系式，同时当批发量为多少件时，工厂获利最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面内，给定不在同一直线上的点A，B，C，如图所示．点O到点A，B，C的距离均等于a（a为常数），到点O的距离等于a的所有点组成图形G，的平分线交图形G于点D，连接AD，CD．

    （1）求证：AD=CD；

    （2）过点D作DEBA，垂足为E，作DFBC，垂足为F，延长DF交图形G于点M，连接CM．若AD=CM，求直线DE与图形G的公共点个数．

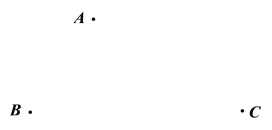
    查看答案和解析>>

    同步练习册答案