
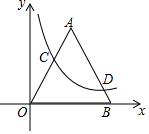 已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点C和点D,则k的值为( )
已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点C和点D,则k的值为( )| A. | $\frac{81\sqrt{3}}{25}$ | B. | $\frac{81\sqrt{3}}{16}$ | C. | $\frac{81\sqrt{3}}{5}$ | D. | $\frac{81\sqrt{3}}{4}$ |
分析 过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,设BD=a,则OC=3a,根据等边三角形的性质结合解含30度角的直角三角形,可找出点C、D的坐标,再利用反比例函数图象上点的坐标特征即可求出a、k的值,此题得解.
解答 解:过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,如图所示.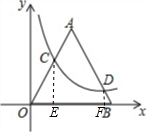
设BD=a,则OC=3a.
∵△AOB为边长为6的等边三角形,
∴∠COE=∠DBF=60°,OB=6.
在Rt△COE中,∠COE=60°,∠CEO=90°,OC=3a,
∴∠OCE=30°,
∴OE=$\frac{3}{2}$a,CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=$\frac{3\sqrt{3}}{2}$a,
∴点C($\frac{3}{2}$a,$\frac{3\sqrt{3}}{2}$a).
同理,可求出点D的坐标为(6-$\frac{1}{2}$a,$\frac{\sqrt{3}}{2}$a).
∵反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点C和点D,
∴k=$\frac{3}{2}$a×$\frac{3\sqrt{3}}{2}$a=(6-$\frac{1}{2}$a)×$\frac{\sqrt{3}}{2}$a,
∴a=$\frac{6}{5}$,k=$\frac{81\sqrt{3}}{25}$.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征、等边三角形的性质以及解含30度角的直角三角形,根据等边三角形的性质结合解含30度角的直角三角形,找出点C、D的坐标是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,∠B=60°,点E、F分别是边BC、AB上的点,且DF垂直平分AE,若BF=1,且EF⊥AB,则线段AD的长为$\sqrt{3}+$3.
如图,在?ABCD中,∠B=60°,点E、F分别是边BC、AB上的点,且DF垂直平分AE,若BF=1,且EF⊥AB,则线段AD的长为$\sqrt{3}+$3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0<m<$\frac{1}{3}$ | B. | -$\frac{1}{3}$<m<0 | C. | m<0 | D. | m>$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
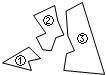 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,现有以下几个方案:
如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,现有以下几个方案:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
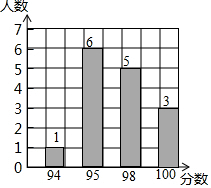 某校“我是小小演说家”演讲比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某校“我是小小演说家”演讲比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )| A. | 95,95 | B. | 6,5 | C. | 95,98 | D. | 100,98 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com