
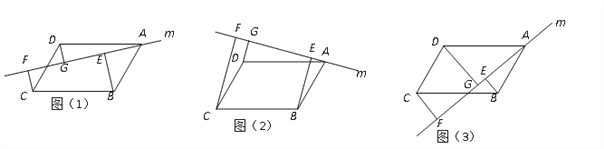
【题目】已知□ABCD中,直线m绕点A旋转,直线m不经过B、C、D点,过B、C、D分别作BE⊥m于E, CF⊥m于F, DG⊥m于G.
(1)当直线m旋转到如图1位置时,线段BE、CF、DG之间的数量关系是 _;
(2)当直线m旋转到如图2位置时,线段BE、CF、DG之间的数量关系是 _;
(3)当直线m旋转到如图3的位置时,线段BE、CF、DG之间有怎样的数量关系?请直接写出你的猜想,并加以证明.
【答案】见解析
【解析】解:
(1)如图1,过C作CM⊥DG,交DG的延长线于点M,

∵DM⊥CM,CF⊥AF,CM⊥DG,
∴∠DMC=∠CFG=∠AEB=90°,
∴四边形GFCM为矩形,
∴FG∥CM,FC=GM,
∵四边形ABCD为平行四边形,
∴CD=AB,CD∥AB,
∴∠DOG=∠BAE=∠DCM,
在△CDM和△ABE中
![]()
∴△CDM≌△ABE(AAS),
∴DM=BE,
∴BE=DG+GM=CF+DG,
故答案为:BE=CF+DG;
(2)如图2,过D作DN⊥CF,交CF于点N,延长CD交AF于点P,
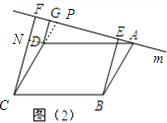
∵DG⊥AF,CF⊥AF,
∴四边形DGFN为矩形,
∴ND∥AF,且DG=NF,
∵四边形ABCD为平行四边形,
∴AB=CD,且AB∥CD,
∴∠CDN=∠DPG=∠BAE,
在△CDN和△BAE中
![]()
∴△CDN≌△BAE(AAS),
∴CN=BE,
∴CF=CN+DF=BE+DG,
故答案为:CF=BE+DG;
(3)猜想:DG=BE+CF;
证明:如图3,过C作CH⊥DG于H,
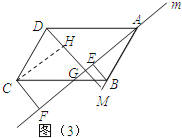
又∵CF⊥m,DG⊥m,
∴四边形CFGH是矩形,
∴CF=HG,
∵DG⊥m,BE⊥m,
∴∠DGE=∠BEG=90°,
∴DG∥BE,
∴∠ABE=∠AMG
∵□ABCD,
∴AD∥BC,CD=AB,
∴∠CDH=∠AMG,
∴∠CDH=∠ABE,
在△CDH和△ABE中
![]()
∴△CDH≌△ABE(AAS),
∴DH=BE,
∴DG=DH+HG=BE+CF,
∴DG=BE+CF.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
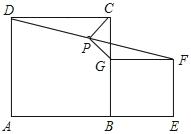
问题:如图所示,在正方形ABCD和BEFG中,点A,B,E在同一直线上,P是线段DF中点,连接PG,PC.
探究:当PG与PC的夹角为90°时,平行四边形BEFG是正方形.
小聪同学的思路是:首先可以证明四边形BEFG是矩形,然后延长GP交DC于点H,构造全等三角形,经过推理可以探索出问题答案.
请你参考小聪同学的思路,探究并解决这个问题.
(1)求证:四边形BEFG是矩形;
(2)求证:PG与PC的夹角为90°时,四边形BEFG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是 ( )
A. 6a+a=6a2 B. -2a+5b=3ab C. 4m2n-2mn2=2mn D. 3ab2-5b2a=-2ab2
查看答案和解析>>
科目:初中数学 来源: 题型:
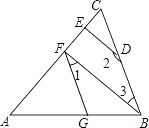
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com