
分析 根据特殊角的三角函数值计算即可.
解答 解:(1)cos260°+sin260°=1;
(2)$\frac{cos45°}{sin45°}$-tan45°=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}$-1=0;
(3)sin60°×cos30°+$\frac{1}{2}$=$\frac{1}{2}×\frac{1}{2}$$+\frac{1}{2}$=$\frac{3}{4}$;
(4)sin45°+$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$$+\frac{\sqrt{2}}{2}$=$\sqrt{2}$;
(5)cos245°+tan60°×cos30°=($\frac{\sqrt{2}}{2}$)2+$\sqrt{3}×\frac{\sqrt{3}}{2}$=2;
(6)$\frac{1-cos30°}{sin60°}$+tan30°=$\frac{1-\frac{\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}$+$\frac{\sqrt{3}}{3}$=$\sqrt{3}$-1;
(7)sin45°cos60°-cos45°=$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$-$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{4}$;
(8)$\sqrt{3}$sin60°+tan60°-2cos230°=$\sqrt{3}×\frac{\sqrt{3}}{2}$+$\sqrt{3}$-2×($\frac{1}{2}$)2=$\sqrt{3}$.
点评 本题考查了特殊角的三角函数值,实数的运算,熟记特殊角的三角函数值是解题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知直线y=x+3的图象与 x轴、y轴交于A,B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分,求直线l的解析式.
如图所示,已知直线y=x+3的图象与 x轴、y轴交于A,B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分,求直线l的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -30 | +80 | -20 | +100 | -96 | +35 | -24 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
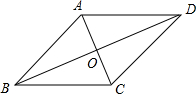 如图,在四边形ABCD中,AB∥DC,对角线AC与BD相交于点O,AO=CO.请你再添一个条件,就能推出四边形ABCD是菱形,则下列条件不符合的是( )
如图,在四边形ABCD中,AB∥DC,对角线AC与BD相交于点O,AO=CO.请你再添一个条件,就能推出四边形ABCD是菱形,则下列条件不符合的是( )| A. | BD平分∠ABC | B. | AB=AD | C. | AC⊥BD | D. | OB=OA |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
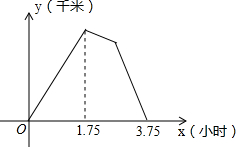 成渝两地山水相连风俗相通,人口、贸易往来频繁,“成渝高铁”的开通更是加速了成渝两地的“同城化进程”.已知两地相距350千米,现有一直达高铁往返于两城市之间,该高铁每次到达成都、重庆后均需停留1小时再重新出发.暑假期间,重庆市铁路局计划在同线路上临时加开一辆慢速直达旅行专列.在试运行期间,该旅行专列与高铁同时从重庆出发,在整个行驶过程中,两车均保持各自速度匀速行驶,经过3.75小时两车第一次相遇.已知两车之间的距离y(千米)与行驶时间x(小时)之间的部分函数关系如图所示,当两车第二次相遇时,该旅行专列共行驶了275千米.
成渝两地山水相连风俗相通,人口、贸易往来频繁,“成渝高铁”的开通更是加速了成渝两地的“同城化进程”.已知两地相距350千米,现有一直达高铁往返于两城市之间,该高铁每次到达成都、重庆后均需停留1小时再重新出发.暑假期间,重庆市铁路局计划在同线路上临时加开一辆慢速直达旅行专列.在试运行期间,该旅行专列与高铁同时从重庆出发,在整个行驶过程中,两车均保持各自速度匀速行驶,经过3.75小时两车第一次相遇.已知两车之间的距离y(千米)与行驶时间x(小时)之间的部分函数关系如图所示,当两车第二次相遇时,该旅行专列共行驶了275千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC.
如图,已知△ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com