
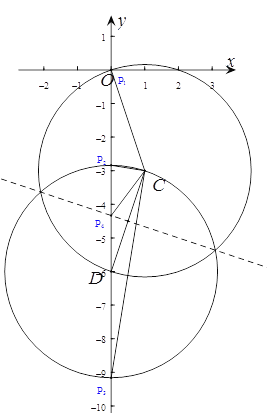
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,点C(1,n)在直线AB上,点D在y轴的负半轴上,且CD=![]() .
.
(1)求点C、点D的坐标.
(2)若P为y轴上的点,当△PCD为等腰三角形时,求点P的坐标.
(3)若点M为x轴上一动点(点M不与点O重合),N为直线y=2x-5上一动点,是否存在点M、N,使得△AMN与△AOB全等?若存在,求出点N的坐标;若不存在,请说明理由.


图1 图2
【答案】(1)C(1,-3),D(0,-6);(2)P(0, ![]() ) 、P(0,
) 、P(0, ![]() ) 、P(0,0)、P(0,
) 、P(0,0)、P(0, ![]() );(3)N(5,5)或N(
);(3)N(5,5)或N(![]() )或N(
)或N(![]() ).
).
【解析】试题分析:(1)先确定点C的坐标,设点D坐标为(0,d)(d<0),则有CD2=(1-0)2+(-3-d)2=![]() ,解之即可得;
,解之即可得;
(2)分别以点C、点D为圆心,CD为半径画圆,圆与y轴即为满足条件的点,作CD的中垂线与y轴的交点也满足条件,然后根据CD的长以及等腰三角形的性质即可得;
(3)分△AM1N1≌△AOB与△AM1N1≌△ABO两种情况,画出相应的图形进行求解即可得.
试题解析:(1)当x=1时,y=2x-5=-3,所以C(1,-3),
设点D坐标为(0,d)(d<0),则有CD2=(1-0)2+(-3-d)2=![]() ,解得:d=0(舍去)或d=-6,所以D(0,-6);
,解得:d=0(舍去)或d=-6,所以D(0,-6);
(2)当P1C=CD时,由(1)计算可知此时P1与原点O重合,所以P1(0,0),
当PC为底时,如图,此时PD=CD=![]() ,所以P2(0,-6-
,所以P2(0,-6-![]() )、P3(0,-6+
)、P3(0,-6+![]() ),
),
当CD为底边时,设P点坐标为(0,p),由题意则有(-3-p)2+12=(-6-p)2,解得:p=![]() ,所以P4(0,
,所以P4(0, ![]() ),
),
综上,点P坐标为: P1(0,0)、P2(0, ![]() ) 、P3(0,
) 、P3(0, ![]() )、P4(0,
)、P4(0, ![]() );
);
(3)由y=2x-5与x轴和y轴分别交于点A和点B可知OA=2.5,OB=5,AB=![]() ,
,
如图所示,当△AM1N1≌△AOB时,AM=AO,M1N1=OB,所以N1(5,5),
当△AM1N1≌△ABO时,AN3=AO=2.5,过点N3作N3E2⊥OA,
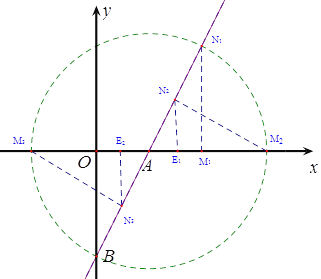
则有△AE2N3∽△AOB,∴![]() ,
,
即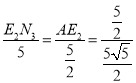 ,∴E2N3=
,∴E2N3=![]() ,AE2=
,AE2=![]() ,
,
同理E1N2=![]() ,AE1=
,AE1=![]() ,
,
∴N3(![]() ),N2(
),N2(![]() ),
),
综上,点N的坐标为:N1(5,5),N2(![]() ),N3(
),N3(![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )

A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
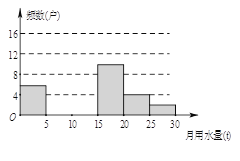
请解答以下问题:
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)填空: ![]() ,
, ![]() ,并把频数分布直方图补充完整;
,并把频数分布直方图补充完整;
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“
(4)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量![]() (个)与加工时间
(个)与加工时间![]() (分)之间的函数关系,观察图象解决下列问题:
(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是________,B点表示的实际意义是___________ _____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用6天;③若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.试问:
(1)两队单独做各要几天完成?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全下列各题解题过程.
如图,EF∥AD,∠1 = ∠2,∠BAC = 70°,求 ∠AGD 的度数.

解:∵EF∥AD ( 已知 )
∴∠2 = ( )
又∵∠1=∠2 ( )
∴∠1=∠3 ( )
∴AB∥ ( )
∴∠BAC + = 180°( )
∵∠BAC = 70°(已知 )
∴∠AGD = _ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com