Question

19．有一张面积为20的三角形纸片，其中一边为AB为8，把它剪成两刀拼成一个矩形（无缝隙、无重叠），且矩形的一边与AB平行，则矩形的周长为18或21．

Answer 1

分析 画出符合的两种图形，根据面积求出高CD长，根据中位线求出矩形的一条边长，再根据矩形的性质求出四条边的长，即可求出矩形的周长．

解答 解：分为两种情况：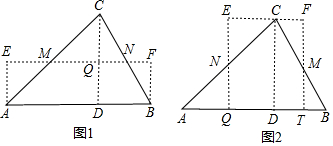
①如图1，延MN剪开，再延CQ剪开（CD⊥AB于D，MN为中位线，CD交MN于Q），△CQN放在△BFN位置上，△CQM放在△AEM位置上，
由三角形面积公式得：20=$\frac{1}{2}$×8×CD，
解得：CD=5，
∵MN为中位线，
∴CQ=DQ=$\frac{1}{2}$CD=2.5，
即矩形AEFB的四边的长为2.5、8、2.5、8，周长为2.5+8+2.5+8=21；
②如图2，延NQ、MT剪开（N、M分别为AC、BC中点，EQ⊥BA于Q，FT⊥AB于T），CD⊥AB于D，△AQN放在△CEN位置上，△BTM放在△CFM位置上，
由三角形面积公式得：20=$\frac{1}{2}$×8×CD，
解得：CD=5，
∵N为AC中点，CD∥EQ，
∴AQ=DQ，
同理BT=DT，
∴QT=$\frac{1}{2}$AB=4，
即矩形EQTF的四边的长为5、4、5、4，周长为5+4+5+4=18；
故答案为：18或21．

点评 本题考查了三角形的中位线定理，矩形的性质，三角形的面积等知识点，能画出符合的两种图形是解此题的关键．