
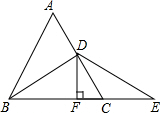
 如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DF⊥BE,垂足是F,求证:BF=EF.
如图,等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DF⊥BE,垂足是F,求证:BF=EF. 分析 要证F是BE的中点,根据题意可知,证明△BDE为等腰三角形,利用等腰三角形的三线合一的性质即可得证.
解答 证明:∵在等边△ABC,且D是AC的中点,
∴∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,∠ACB=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E,
∴∠E=30°,
∴∠DBC=∠E=30°,
∴BD=ED,△BDE为等腰三角形,
又∵DF⊥BE,
∴F是BE的中点,
∴BF=EF.
点评 本题考查了等腰三角形顶角平分线、底边上的中线和高三线合一的性质以及等边三角形每个内角为60°的知识.辅助线的作出是正确解答本题的关键.


科目:初中数学 来源: 题型:解答题
 同学们,如果通过折纸能析出一个等边三角形,你相信吗?如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下,则△ADH为等边三角形,请你动手试试看,并说明理由.
同学们,如果通过折纸能析出一个等边三角形,你相信吗?如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下,则△ADH为等边三角形,请你动手试试看,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
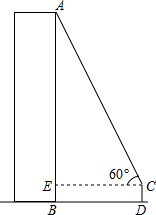 如图.为测量某建筑的高度.在离该建筑底部20.0米处.目测其顶部A点.视线与水平线的夹角为60°.目高1.6米.试利用相似三角形的知识.求出该建筑的高度.(精确到0.1米)
如图.为测量某建筑的高度.在离该建筑底部20.0米处.目测其顶部A点.视线与水平线的夹角为60°.目高1.6米.试利用相似三角形的知识.求出该建筑的高度.(精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}-2$ | D. | $\sqrt{3}+2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
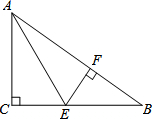 如图,在Rt△ABC中,∠C=90°,BC=5,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).求BE的长.
如图,在Rt△ABC中,∠C=90°,BC=5,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).求BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com