
【题目】如图,已知直线![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() .
.
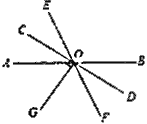
(1)求![]() 的度数.
的度数.
(2)![]() 是
是![]() 的平分线吗?说明你的理由.
的平分线吗?说明你的理由.
【答案】(1)∠AOG=54°;(2)OC是∠AOE的角平分线;理由见解析.
【解析】
(1)由对顶角相等可得∠AOC的度数,由OG⊥CD可得∠COG=∠DOG=90°,利用角的和差关系即可求出∠AOG的度数;
(2)根据角平分线的定义可得∠AOG=∠FOG,利用角的和差关系可得∠FOD=∠AOC,根据对顶角相等,利用等量代换可得∠AOC=∠EOC,即可得答案.
(1)∵∠AOC和∠BOD是对顶角,∠BOD=36°,
∴∠AOC=∠BOD=36°,
∵OG⊥CD,
∴∠COG=∠DOG=90°,
∴∠AOG=∠COG-∠AOC=90°-36°=54°.
(2)OC是∠AOE的角平分线,理由如下:
∵OG是∠AOF的角平分线,
∴∠AOG=∠FOG,
∵∠COG=∠DOG=90°,
∴∠COG-∠AOG=∠DOG-∠FOG,即∠AOC=∠FOD,
∵∠EOC和∠FOD是对顶角,
∴∠EOC=∠FOD,
∴∠AOC=∠EOC,
∴OC是∠AOE的角平分线.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() )两点与x轴,y轴分别交于A、B(0,2)两点,如果
)两点与x轴,y轴分别交于A、B(0,2)两点,如果![]() 的面积为6.
的面积为6.
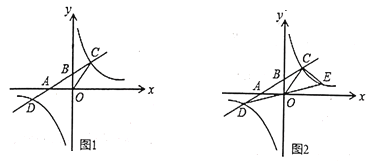
(1)求点A的坐标;
(2)求一次函数和反比例函数的解析式;
(3)如图2,连接DO并延长交反比例函数的图象于点E,连接CE,求点E的坐标和![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
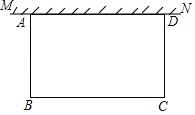
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:

(1)阿中总共剪开了几条棱?
(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);
(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某长方形广场长为a米,宽为b米;广场的中间圆形绿地的半径为![]() 米;广场的死角都有一块半径相同的四分之一圆形的绿地,且圆形绿地的半径也为
米;广场的死角都有一块半径相同的四分之一圆形的绿地,且圆形绿地的半径也为![]() 米;
米;

(1)请用代数式分别表示绿地的总面积和空地的面积(结果保留π);
(2)若长方形长为500米,宽为300米,求广场空地的面积。(π取3.14,并保留两个有效数学)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=![]() BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
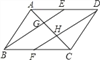
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用长度相同的小木棒按一定规律搭成的图形.图①用5根小木棒搭了一个五边形;图②用9根小木棒搭了两个五边形;图③用13根小木棒搭了三个五边形;……

(1)按此规律搭下去,搭第n个图形用了 根小木棒;(直接写出结果)
(2)是否存在某个图恰好用了2 019根小木棒?如果存在,试求是第几个图形?如果不存在,试求用2019根小木棒按图示规律最多能搭多少个五边形?还剩余多少根小木棒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com