
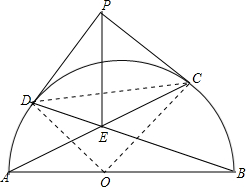
 如图所示,AB是半圆O的直径,过点A、B分别作弦AC与BD相交于点E,又过C、D两点引圆的切线交于点P,连结PE,试证:PE⊥AB.
如图所示,AB是半圆O的直径,过点A、B分别作弦AC与BD相交于点E,又过C、D两点引圆的切线交于点P,连结PE,试证:PE⊥AB. 分析 连接AD、BC并延长相交于Q,根据圆周角定理证得AC、BD是三角形ABQ两条边上的高,从而证得点E是三角形ABQ的三条高的交点,连接QE,则QE⊥AB,取QE中点F,连接FD和FC,OD和OC,然后证得P和F是同一点即可.
解答  解:连接AD、BC并延长相交于Q,
解:连接AD、BC并延长相交于Q,
∵AB是直径,
∴AC、BD是三角形ABQ两条边上的高,
∴点E是三角形ABQ的三条高的交点,
连接QE,则QE⊥AB,
取QE中点F,连接FD和FC,OD和OC,则FD=$\frac{1}{2}$QE=FQ
∴∠QDF=∠DQF
∵∠DQF+∠QAB=90°,∠DBA+∠QAB=90°,OA=OD,
∴QAB=∠ODB,
∴∠QDF=∠DQF=∠DBA=∠ODB
∴∠ODF=∠ODB+∠FDE=∠QDF+∠FDE=90°,即OD⊥DF,
同理可证OC⊥CF
∴DF和CF就是经过D、C两点的圆O的切线,
∴F点和P点重合,
∴PE⊥AB.
点评 本题考查了圆周角定理,三角形斜边中线的性质,三角形的性质以及切线的判定作出辅助线构建直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
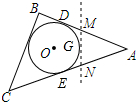 如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是12cm.
如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是12cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com