
 (2012•南平)如图所示,水平放置的长方体底面是长为4和宽为2的矩形,它的主视图的面积为12,则长方体的体积等于( )
(2012•南平)如图所示,水平放置的长方体底面是长为4和宽为2的矩形,它的主视图的面积为12,则长方体的体积等于( )科目:初中数学 来源: 题型:
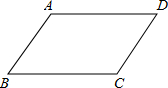 件中,选择添加一个恰当的条件.使四边形AECF是平行四边形,并予以证明,
件中,选择添加一个恰当的条件.使四边形AECF是平行四边形,并予以证明,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•南平)如图,直线l与⊙O交于C、D两点,且与半径OA垂直,垂足为H,已知OD=2,∠O=60°,
(2012•南平)如图,直线l与⊙O交于C、D两点,且与半径OA垂直,垂足为H,已知OD=2,∠O=60°,查看答案和解析>>
科目:初中数学 来源: 题型:
 其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)
其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com