
【题目】如图,在半径为![]() 的
的![]() 中,
中,![]() 是直径,点
是直径,点![]() 是
是![]() 中点,连接
中点,连接![]() ,交
,交![]() 于点
于点![]() ,弦
,弦![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
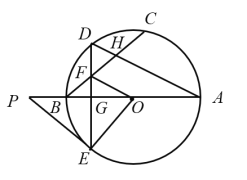
(1)求![]() 的长;
的长;
(2)连接![]() ,求证:
,求证:![]() ;
;
(3)当点![]() 在
在![]() 上运动时,连接
上运动时,连接![]() ,
,![]() ,求
,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
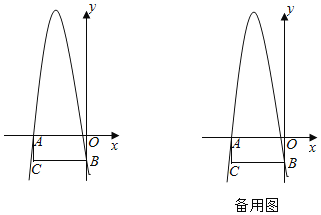
【题目】如图,在平面直角坐标系中,矩形AOBC的边AO在x轴的负半轴上,边OB在y轴的负半轴上.且AO=12,OB=9.抛物线y=﹣x2+bx+c经过点A和点B.
(1)求抛物线的表达式;
(2)在第二象限的抛物线上找一点M,连接AM,BM,AB,当△ABM面积最大时,求点M的坐标;
(3)点D是线段AO上的动点,点E是线段BO上的动点,点F是射线AC上的动点,连接EF,DF,DE,BD,且EF是线段BD的垂直平分线.当CF=1时.
①直接写出点D的坐标 ;
②若△DEF的面积为30,当抛物线y=﹣x2+bx+c经过平移同时过点D和点E时,请直接写出此时的抛物线的表达式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为![]() 的网格中,点
的网格中,点![]() ,点
,点![]() 均落在格点上,
均落在格点上,![]() 为⊙
为⊙![]() 的直径.
的直径.
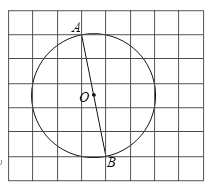
(1)![]() 的长等于__________;
的长等于__________;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以![]() 为斜边、面积为
为斜边、面积为![]() 的
的![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
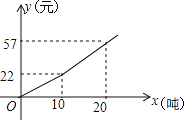
【题目】为鼓励市民节约用水,某市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系
(1)小红家五月份用水8吨,应交水费_____元;
(2)按上述分段收费标准,小红家三、四月份分别交水费36元和19.8元,问四月份比三月份节约用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
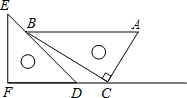
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
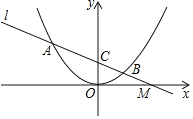
【题目】如图,已知抛物线y=ax2过点A(﹣3,![]() ).
).
(1)求抛物线的解析式;
(2)已知直线l过点A,M(![]() ,0)且与抛物线交于另一点B,与y轴交于点C,求证:MC2=MAMB;
,0)且与抛物线交于另一点B,与y轴交于点C,求证:MC2=MAMB;
(3)若点P,D分别是抛物线与直线l上的动点,以OC为一边且顶点为O,C,P,D的四边形是平行四边形,求所有符合条件的P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com