

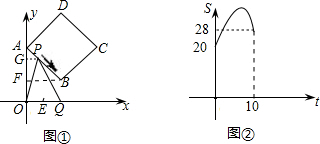
 解:(1)作BF⊥y轴于F.
解:(1)作BF⊥y轴于F. =
=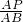 ,即
,即
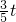 ,OG=10-
,OG=10-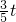 ,
, OQ•OG,
OQ•OG, (t+4)(10-
(t+4)(10- t),
t), t+20,
t+20,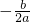 =-
=- =
=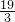 ,
,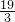 在0≤t≤10内,
在0≤t≤10内,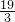 时,S有最大值,此时GP=
时,S有最大值,此时GP= t=
t=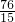 ,
,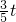 =
=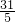 ,
, ).
). OQ•OG,再把OQ•OG的值代入即可得出S=-
OQ•OG,再把OQ•OG的值代入即可得出S=- t+20
t+20

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
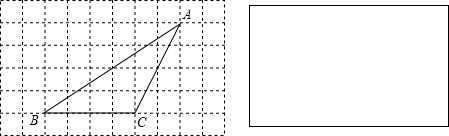
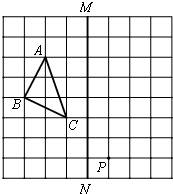 21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)查看答案和解析>>
科目:初中数学 来源: 题型:
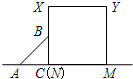 (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com