
| A. | ±1 | B. | ±3 | C. | ±1或3 | D. | ±1或±3 |
分析 根据绝对值的性质,将绝对值符号去掉,然后计算.由于不知道a、b、c的符号,故需分类讨论.
解答 解:对a,b,c的取值情况分类讨论如下:
①当a,b,c都是正数时,$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$=$\frac{a}{a}+\frac{b}{b}+\frac{c}{c}$=1+1+1=3;
②当a,b,c都是负数时,$\frac{|a|}{a}=\frac{b}{|b|}=\frac{|c|}{c}$=-1,所以和为-3;
③当a,b,c中有两个正数,一个负数时,$\frac{|a|}{a},\frac{b}{|b|},\frac{|c|}{c}$有两个1,一个-1,所以和为1.
④当a,b,c中有一个正数、两个负数时,$\frac{|a|}{a},\frac{b}{|b|},\frac{|c|}{c}$中有两个-1,一个+1,所以和为-1.
故$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$=±1或±3,
故选:D.
点评 本题考查了绝对值,解决本题的关键是进行分类讨论,分类讨论时要全面,要做到不重复不遗漏.规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.


科目:初中数学 来源: 题型:解答题
 已知:如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,AC⊥BC,OA=2,OB=8,设顶点为D.
已知:如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,AC⊥BC,OA=2,OB=8,设顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一慢车和一快车沿同一路线从A地驶往B地,根据图象求:
一慢车和一快车沿同一路线从A地驶往B地,根据图象求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题:
一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系.根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
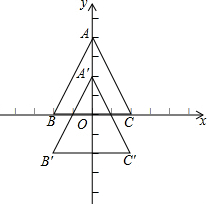 如图所示,已知△ABC三个顶点的坐标分别是A(0,4),B(-2,0),C(3,0),把△ABC沿y轴向下平移2个单位得△A′B′C′
如图所示,已知△ABC三个顶点的坐标分别是A(0,4),B(-2,0),C(3,0),把△ABC沿y轴向下平移2个单位得△A′B′C′查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com